生物控制系统建模

我的预期是把这篇文章搞成新学生进组的 Guide , 结果发现写起来特别花时间. 本来想双休日一口气写完, 现在看来只能做业余项目慢慢写了.

再吐槽一下, NMA 把绘图程序都搞成 Helper Function 了, 看似封装了细节, 实则增加了理解成本, 而且还和日常分析数据的 Workflow 不符, 我觉得这个设计不妥.

版权声明: 本文档来源于 NeuromatchAcademy 课程第二周内容, 并依照原内容所声明的 CC-BY-4.0 协议, 保留对原内容进行修改, 甚至利用其进行商业行为的权利. 本文档是对 NMA 课程原内容基础上的演绎, 并同样遵守 CC-BY-4.0 协议.

1. 概述

心理学研究的本质是尝试理解和预测人的内部心理过程. 然而由于内部过程的不可观测性, 我们会通过测量外部的信号或行为来反推这一黑箱的内部. 换句话说, 理解个体心理的过程, 实质上就是理解个体的行为和生物信号背后的控制系统的过程. 而在控制论等知识的指导下, 我们利用数学工具对内部的控制过程进行建模, 以帮助我们解释和预测外部所观测到的变量.

对控制系统的建模需要两种数学工具:

• 贝叶斯统计
• 线性系统

贝叶斯概率可以用来描述生物不断从外部积累信息以理解世界的过程. 而线性系统则可以描述生物行为的部分特征.

2. 贝叶斯统计

在执行任何行为前, 我们都需要对外部世界有一个基础的认识 (i.e. 我们需要指导对面的沟离有多宽, 我们要跳多远才能跳过去, 否则就会掉进沟里). 但外部世界对我们来说是不确定的, 同时整个系统中还存在大量的噪声干扰. 因此我们需要不断收集信息并进行推断, 才能准确理解外部世界中的信息.

贝叶斯概率是我们理解信息积累与推断过程的有力工具. 从贝叶斯统计的角度来看, 概率是指某个事件发生的概率. 根据贝叶斯法则, 我们可以将不断输入的外部信息更新到我们的现有的信念当中. 而通过贝叶斯统计思想, 使用概率分布对概率进行描述, 我们则能够将不确定性本身加入到我们的模型当中.

在计算贝叶斯概率前, 我们需要先回忆概率论中的基本概念与计算法则, 包括:

联合概率

$$ p(x,y) = p(x\ AND\ y) $$

条件概率

$$ p(x \mid y)=\frac{p(x, y)}{p(y)} $$

边缘概率

$$ p(x)=\sum_{y} p(x, y) $$

乘法原则

$$ p(x = 1\ AND\ y = 1) = p(x = 1) \times p(y = 1) $$

加法原则 $$ p(x = 1\ OR\ y = 1) = p(x = 1) + p(y = 1) $$

链式法则

$$ P(a, b, c) =P(a \mid b, c)P(b, c) =P(a \mid b, c)P(b \mid c)P(c) $$

公式推导与应用不作具体介绍. 如果对这些知识陌生, 建议观看 Coursera 上的 概率图模型课程 .

而贝叶斯法则是我们最重要的公式, 描述了我们在收集数据(D)的情况下对假设(H)的认识.

$$ P(H \mid D)=\frac{P(D \mid H) P(H)}{P(D)} \qquad P(D)=\sum_{H} P(D \mid H) P(H) $$

在这个公式的框架下, 我们可以衍生一系列的概念, 包括贝叶斯决策与推断(interface).

贝叶斯决策可以用来描述生物体内部对客观事物价值. 主观概念下, 我们对某个事物的价值认识是非线性的. (i.e. 大街上丢 1 元与 100 元, 心疼程度是非线性的). 因此对某个事物的价值的认识, 存在效用函数 U(结果, 条件)来描述. 因此对某个行为的价值可以使用如下公式进行描述:

$$ V_{c}(a)=\sum_{o, c} U(o, c) P(o \mid a) P(c) $$

其中, a 代表行为 (action), o 代表获益 (outcome), c 代表外部环境 (context). 该公式可以将不确定性纳入对某个行为的价值的考虑.

推断则是指我们在获得了数据后如何计算出特定事件的概率.

接下来让我们借助代码逐步理解这些概念.

2.1 贝叶斯法则计算与高斯分布

贝叶斯概率通过对概率分布的计算来实现, 而高斯分布是描述自然界中事件发生的最常见概率分布. 高斯分布的概率密度公式是:

$$ \mathcal{N}\left(\mu, \sigma^{2}\right)=\frac{1}{\sqrt{2 \pi \sigma^{2}}} \exp \left(\frac{-(x-\mu)^{2}}{2 \sigma^{2}}\right) $$

如果直接理解的话, 你可以把这个公式看作是每个输入值 x 所对应的概率值 p 的函数.

我们首先先写高斯分布的概率密度函数 my_gaussian.

在这里我想说的是, 非常不推荐您在真正的研究中自己编写这些底层的函数. 实际上下面的这段函数我为了写对 (理清这些括号的关系) 花了十几分钟.

my_gaussian <- function(x_points, mu, std){
  px = (1/std*sqrt(2*pi)) * exp((-1 * ((x_points - mu) ^ 2)) / (2 * (std ^ 2))) 
  px = px / sum(px)
  return(px)
}

x <- seq(-8, 9, 0.01)

px = my_gaussian(x, -1, 1)
plot(x, px)

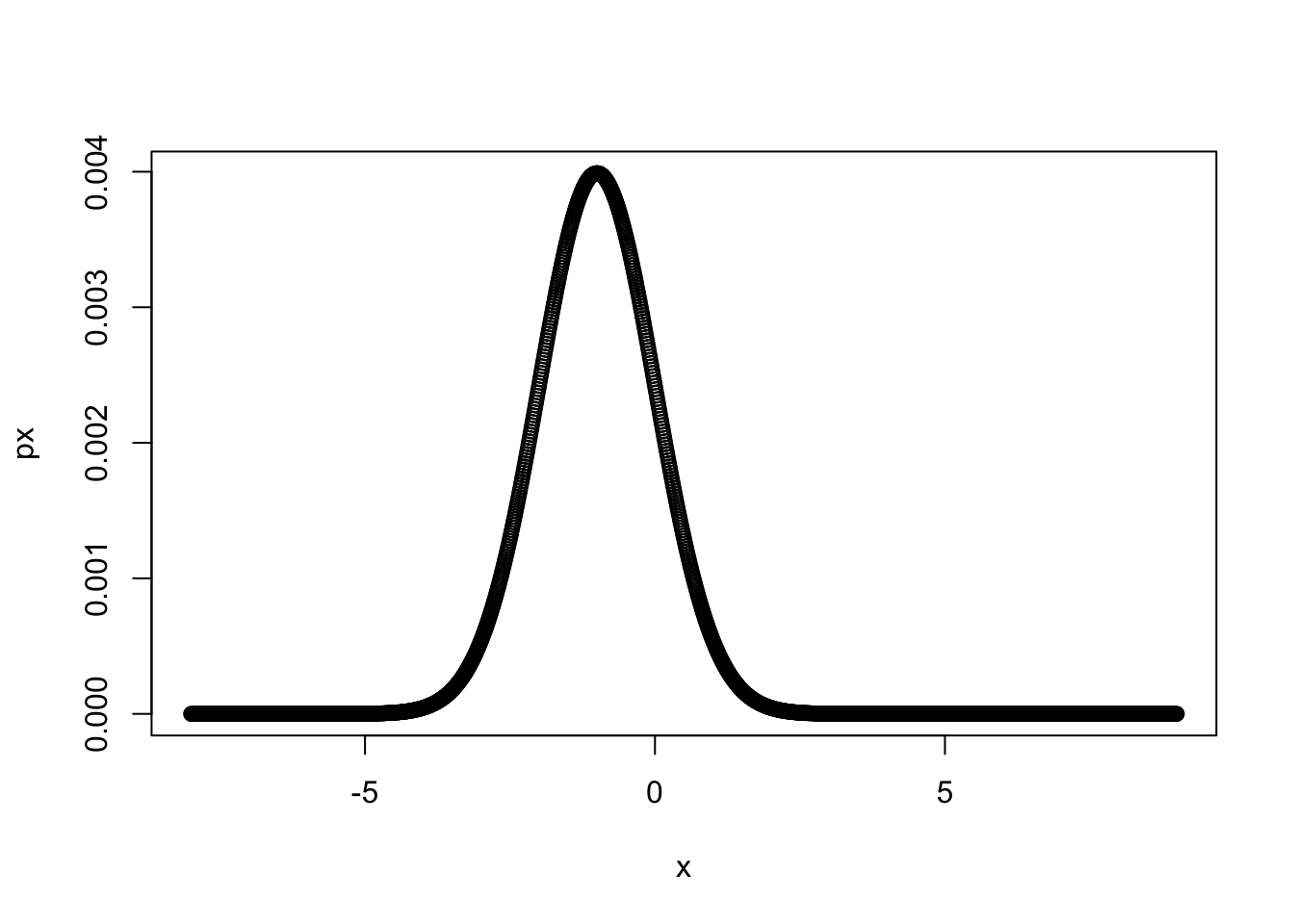
要注意的是, 我们这里有一个强假设, 即在函数中, 我们为了标准化 px 的值, 会假定给定的所有 x, 其 px 值的总和为 1 (概率空间当中所有样本概率的和为 1 , 或概率密度函数图像的面积应为 1 ), 才可以使用 px = px / sum(px) 来进行标准化. 但这实际上是一种近似的方法.

让我们回到贝叶斯公式上. 我们知道贝叶斯法则的概念是:

$$ Posterior =\frac{\text { Likelihood } \times \text { Prior }}{\text { Normalization constant }} $$

其中公式右边的分布是常数项, 因此我们可以省略这一部分的计算, 而将等于改成正比. 假设先验和似然都是正态分布, 我们可以进行如下推导:

$$ Posterior \propto \mathcal{N}\left(\mu_{\text {likelihood}}, \sigma_{\text {likelihood}}^{2}\right) \times \mathcal{N}\left(\mu_{\text {prior}}, \sigma_{\text {prior}}^{2}\right) $$

那么假设我们给定先验分布为$\mathcal{N}\left(-1, 1.5^{2}\right)$, 似然为$\mathcal{N}\left(3, 1.5^{2}\right)$, 让我们试着求一下后验.

如果我们应用前面的 my_gaussian() 函数, 那么实际上就是计算每个离散点的概率. 同时我们如前, 将每个点的累计值近似为1, 那么我们可以得到如下的计算过程:

compute_posterior_pointwise <- function(prior, likelihood){
  posterior = (prior * likelihood) / sum(prior * likelihood)
  return(posterior)
}

bayesian_update_simulation <- function(mu_1, mu_2, sigma_1, sigma_2){
  x = seq(-8, 9, 0.01)
  
  probability_distribution_1 <- my_gaussian(x, mu_1, sigma_1)
  probability_distribution_2 <- my_gaussian(x, mu_2, sigma_2)
  posterior <- compute_posterior_pointwise(probability_distribution_1, probability_distribution_2)
  
  result_table <- cbind(x, probability_distribution_1, probability_distribution_2, posterior)
  
  return(result_table)
}

simulation_data <- bayesian_update_simulation(mu_1 = 3, mu_2 = -1, sigma_1 = 1.5, sigma_2 = 1.5)

head(simulation_data)

##          x probability_distribution_1 probability_distribution_2    posterior
## [1,] -8.00               5.586455e-15               4.964038e-08 8.724337e-19
## [2,] -7.99               5.866226e-15               5.120788e-08 9.450542e-19
## [3,] -7.98               6.159735e-15               5.282254e-08 1.023628e-18
## [4,] -7.97               6.467642e-15               5.448568e-08 1.108637e-18
## [5,] -7.96               6.790638e-15               5.619869e-08 1.200599e-18
## [6,] -7.95               7.129448e-15               5.796299e-08 1.300073e-18

library(ggplot2)
library(tidyverse)

## ─ Attaching packages ──────────────────── tidyverse 1.3.0 ─

## ✓ tibble  3.0.3     ✓ dplyr   1.0.1
## ✓ tidyr   1.1.1     ✓ stringr 1.4.0
## ✓ readr   1.3.1     ✓ forcats 0.5.0
## ✓ purrr   0.3.4

## ─ Conflicts ───────────────────── tidyverse_conflicts() ─
## x dplyr::filter() masks stats::filter()
## x dplyr::lag()    masks stats::lag()

simulation_data %>% 
  data.frame() %>% 
  tidyr::gather(key = "distribution", value = "y", -x) %>% 
  ggplot() + geom_point(aes(x = x, y = y, colour = distribution))

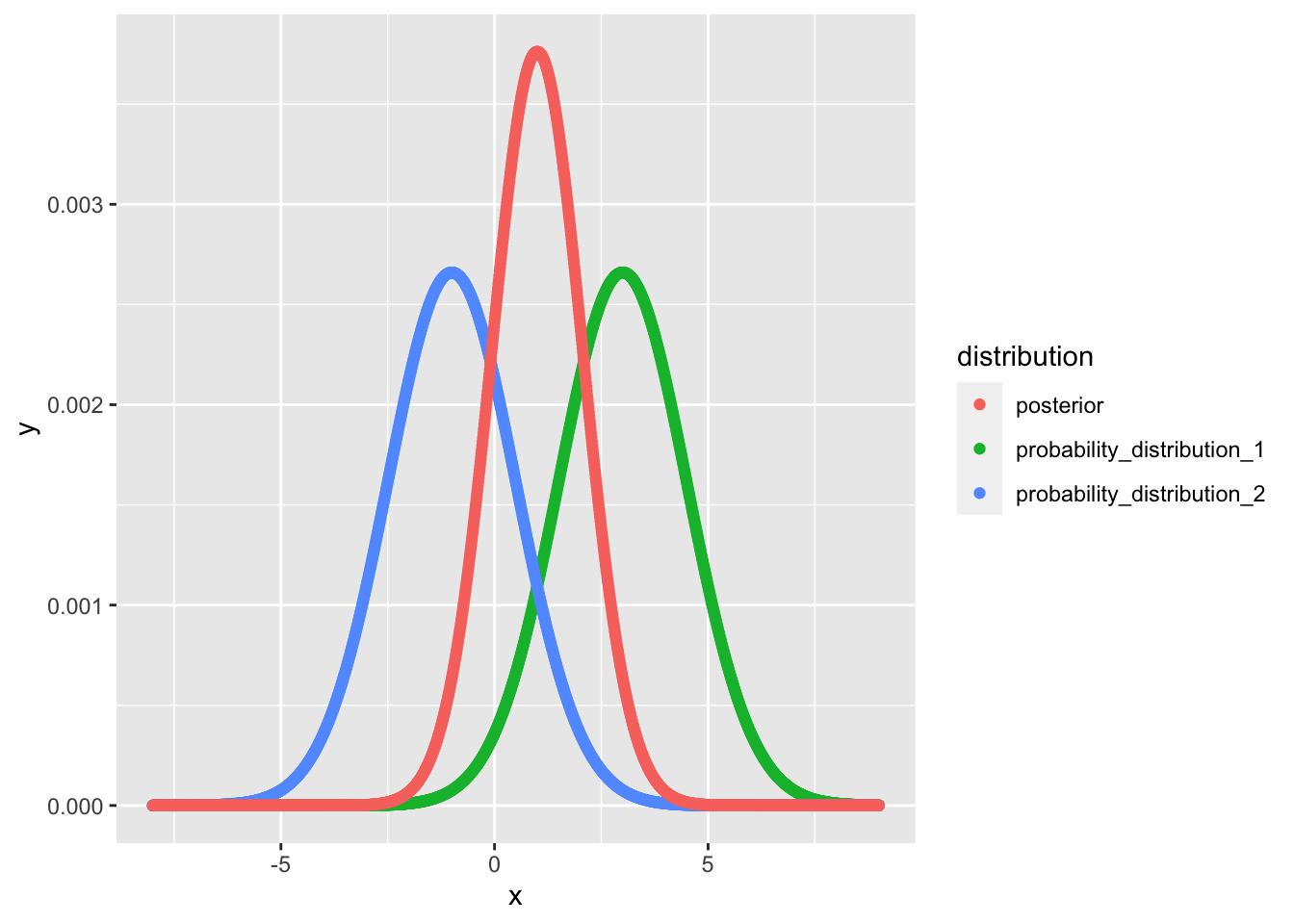
从这张图上, 我们可以很容易看出每个点上的概率更新的过程.

刚刚我们使用的方法被称为网格估计 (grid estimate). 这种方法将整个概率空间分成无数的网格, 而我们的计算过程就是将每个网格的先验概率和似然求出, 再通过相乘的方法, 求出其后验. 事实上, 这是贝叶斯概率计算最常用的方法. 因为你接下来见到的后验解析解 (通过推导公式而计算的结果), 在构建多参数的贝叶斯模型时, 非常难以推导. 不过我们当前的问题还比较简单, 我们可以先尝试一下:

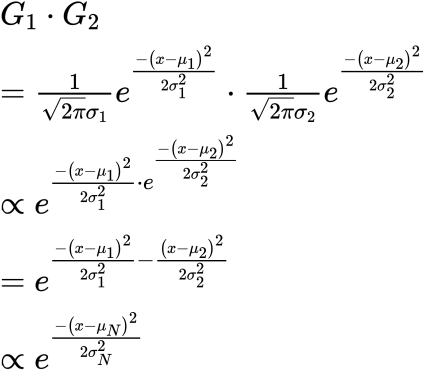
你可能觉得计算过程很难, 事实上的确是这样的. 这一段公式也是我从网上直接抄来的 (为了让你发现这一点我专门截了一个低清版的图, 而不是自己 LaTeX 写下来公式), 而我自己推不出 (至少也是懒得推导) 本公式. 但我想要让你关注的是, 你会发现两个高斯分布乘积的解析解, 仍然是近似高斯分布的形式. 结合上面的图, 我们也会发现图形的形状对于先验与后验并没有发生改变. 我们将这种分布之间的关系称为共轭分布. 共轭分布是一种很重要的性质, 请记住这一特性.

例如, 我们可以利用这一特性, 知道后验分布同样是一个正态分布, 因此对后验的点估计 (分布的 “最佳估计值”) 就是其尖峰处, 因此我们可以使用先验分布和似然的参数mu与sigma, 直接借助公式计算后验的点估计值. 即:

$$ \mu_{new}=\frac{\mu_{1} \frac{1}{\sigma_{1}^{2}}+\mu_{2} \frac{1}{\sigma_{2}^{2}}}{1 / \sigma_{1}^{2}+1 / \sigma_{2}^{2}} $$

2.2 贝叶斯概率是对于估计值及其信念的表征

我们已经理解了贝叶斯的一些基本计算方法, 接下来让我们谈一谈为什么使用贝叶斯来表征心理过程.

想象一下你正在看一场电影, 屏幕上演员的嘴在动, 但你为什么听配音的时候会感觉是屏幕上的演员在说话? 我们知道影院的音响系统, 利用我们的双耳效应, 会使得让你对于声源的定位在屏幕演员的面孔处, 从而让你产生声源在屏幕演员上的感觉. 那么我们的大脑会怎样识别这些信息, 并得到最终的结论呢? 事实上, 我们很难建立起对外部信息的准确认识 (想想看, 如果让你在屏幕上标记你能听到的声源位置, 你会点一个点, 还是画一个圈标记大概范围?), 从而我们会倾向使用分布来去描述. 因此你感知屏幕上的声源位置, 恰好是一个离散程度较大的高斯分布, 而你的视觉信息定位能力强, 因此你会在屏幕演员处得到一个离散程度较小的高斯分布. 当两种信息整合起来后, 你会产生声源是在演员面孔附近的觉知, 从而感觉是屏幕上的演员在说话. 这就是大脑获取环境信息并进行信息更新的整个过程.

更进一步, 你甚至可以尝试将双耳听到的声音的定位分离成两个高斯分布, 然后再和视觉信息共同建模, 看看后验会是什么情况, 是否仍然可以准确定位? (提示: 根据共轭分布的性质, 这个模型的后验分布仍然是一个高斯分布).

2.3 混合高斯分布与概率推断

让我们再想想刚才的例子, 在其中, 我们实际上经历了一个因果推断的过程. 即我们对于声音位置的估计分布和图像位置的估计分布有着极大的重合, 我们便认为声音是屏幕上的嘴发出来的. 这个过程便涉及推断过程.

为了加深我们的理解, 让我们来设计一个更为复杂的例子: 想象我们刚才看电影的场景变成了一场实验, 在一个 Block 当中, 有 65% 的 trials 中声源直接来源于屏幕的演员附近, 而 35% 的 trials 中声源来源于另一个地方. 接下来让我们用概率推断来判别被试认为声源来源的位置.

在这个例子中, 被试的感觉系统感受到两方面的信息:

• 声音的位置作为先验信息
• 环境中的噪声

由于环境中的声源来源于两个地方, 且出现的概率不同, 单一的高斯分布已经无法描述这个定位信息, 在这里我们使用混合高斯分布来对先验进行描述. 混合高斯分布实际上就是对多个高斯分布的组合. 他的公式形式是这样的:

$$ { Mixture } = \left[p_{\text {common}} \times \mathcal{N}\left(\mu_{\text {common}}, \sigma_{\text {common}}\right)\right] +[\underbrace{\left(1-p_{\text {common}}\right)}_{\text {p independent}} \times \mathcal{N}\left(\mu_{\text {independent}}, \sigma_{\text {independent}}\right)] $$

也就是将两个不同的高斯分布组合起来, 并对他们分别乘以先验概率. 要注意的是, 这两个高斯分布所描述的事件应当是互相独立的.

假设我们第一个声源来源于屏幕上 (也就是正对你), 我们可以把这个声源描述成 mu = 0, sigma = 0.5 的高斯分布. 而另一个声源来源于你的左侧, 同时声音离你比较远, 音响效果也不好, 所以我们把声源用 mu = -3, sigma = 1.5 的高斯分布进行描述. 我们前面提到了, 65% 的概率下声源来源于你的面前. 接下来我们仍然仿照前面的例子, 使用网格法来描述这个概率分布:

mixture_prior <- function(x, mu_1, sigma_1, mu_2, sigma_2, p_1){
  gaussian_1 <- my_gaussian(x, mu_1, sigma_1)
  gaussian_2 <- my_gaussian(x, mu_2, sigma_2)
  
  
  temp <- (p_1 * gaussian_1) + ((1 - p_1) * gaussian_2)
  mixture_prior <- temp / sum(temp)
  
  return(mixture_prior)
}

x <- seq(-10, 11, 0.01)

mu_1 = 0
sigma_1 = 0.5
mu_2 = -3
sigma_2 = 1.5
plot(x, mixture_prior(x, mu_1, sigma_1, mu_2, sigma_2, p_1 = 0.65))

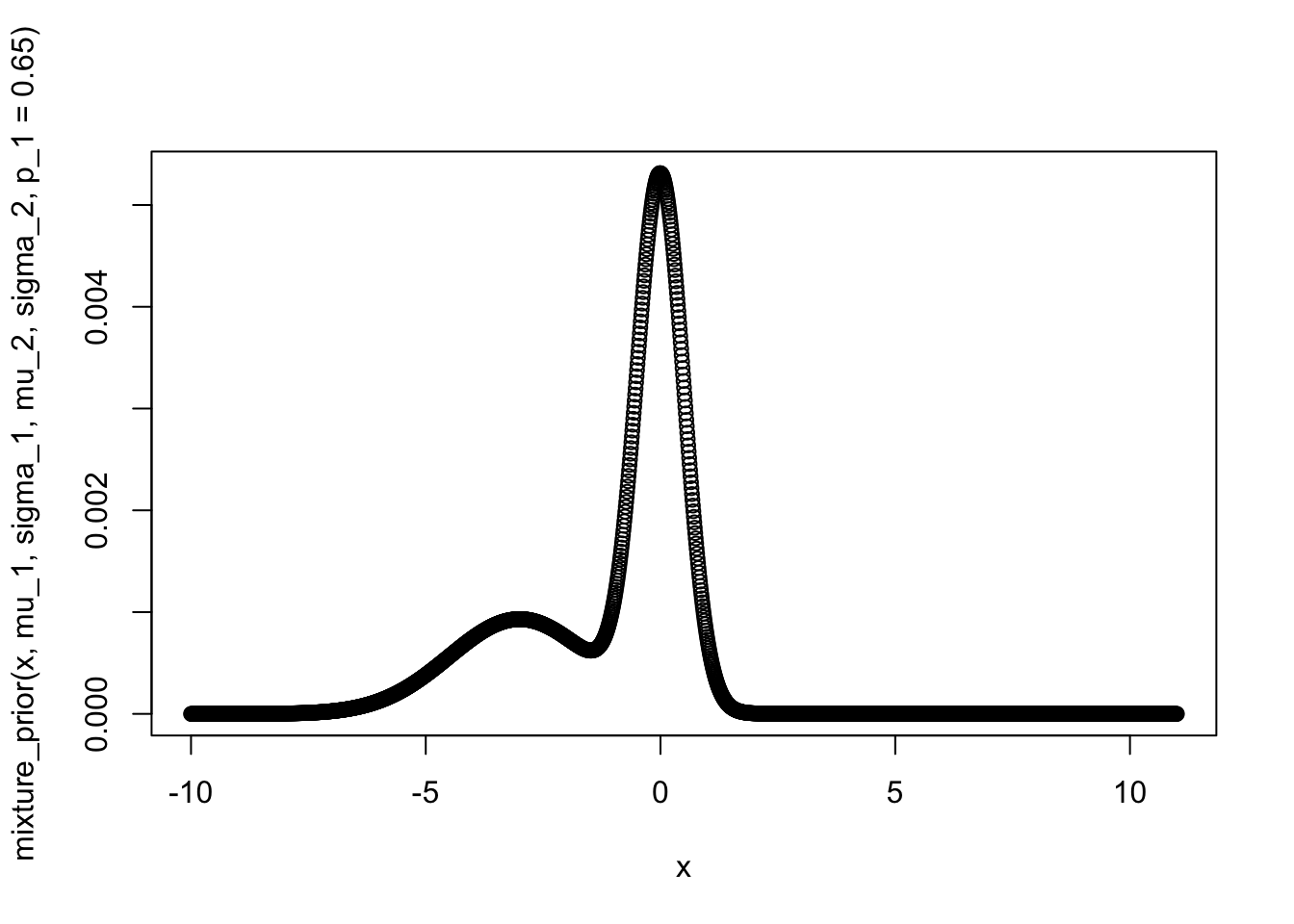
如果我们把单独描述左侧声源的高斯分布画出来, 你会发现先验概率对其的影响:

x <- seq(-10, 11, 0.01)
plot(x, my_gaussian(x, mu_2, sigma_2))

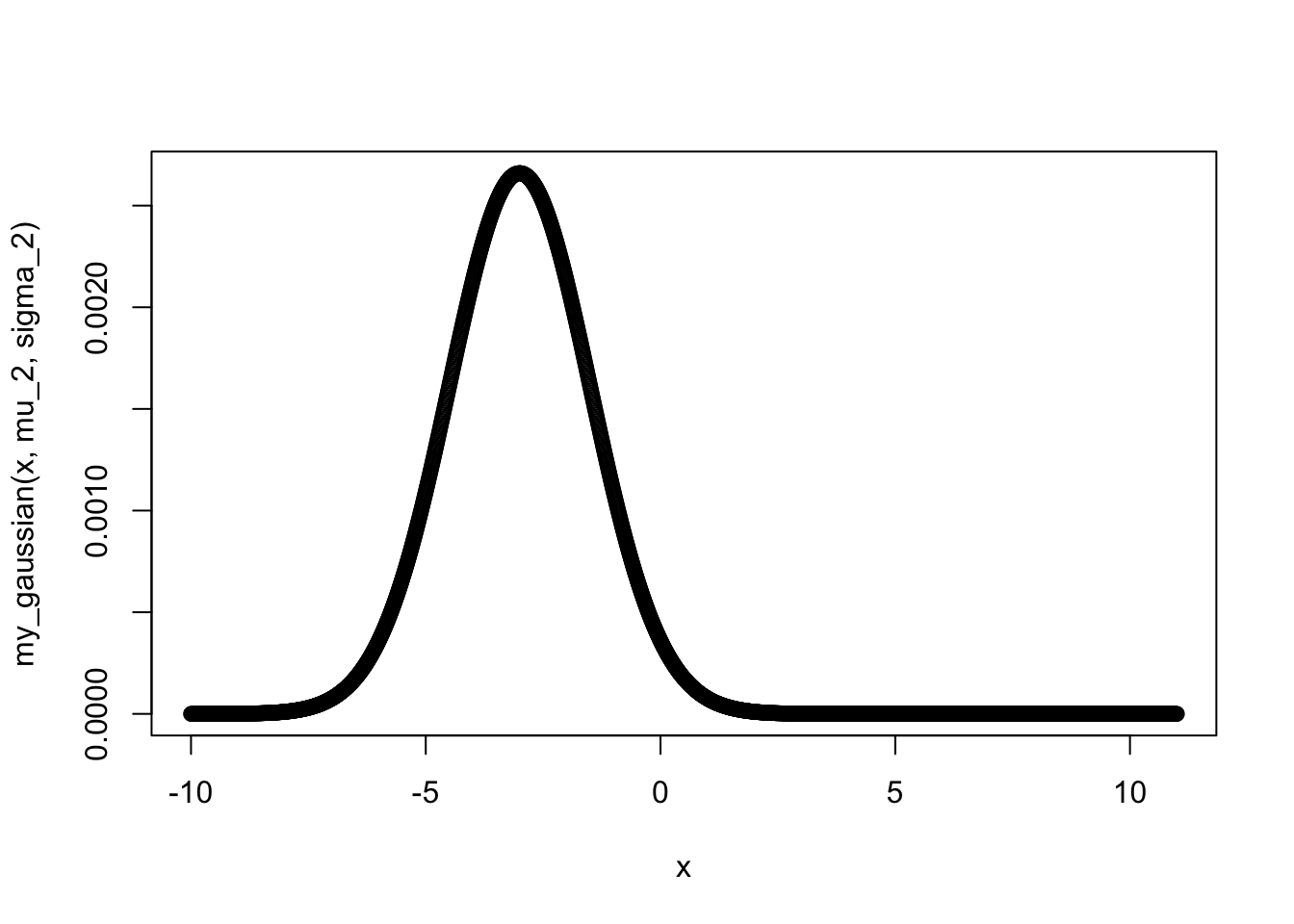
我们可以发现, 外界刺激发生的概率对我们的认知产生了极大的影响. 我们实现的这个混合高斯分布所描述的先验分布, 实际上就是对多个概率分布的加权线性组合.

现在我们再回到之前的问题, 我们除了听到这两处的声音外, 我们同时还看到了屏幕上演员的面孔 (就在你面前, 看的很清楚, 假设这个分布的sigma是0.3吧). 在面孔这个似然信息的加入后, 我们做贝叶斯推断得到的后验信息应该是什么呢?

prior_2_sound_source <- mixture_prior(x, mu_1, sigma_1, mu_2, sigma_2, p_1 = 0.65)
likelihood_vision <- my_gaussian(x, mu = 0, std = 0.3)
posterior_2_sound_source <- compute_posterior_pointwise(prior_2_sound_source, likelihood_vision)

cbind(x, prior_2_sound_source, likelihood_vision, posterior_2_sound_source) %>% 
  data.frame() %>% 
  tidyr::gather(key = "distribution", value = "y", -x) %>% 
  ggplot() + geom_point(aes(x = x, y = y, colour = distribution), alpha = 0.5)

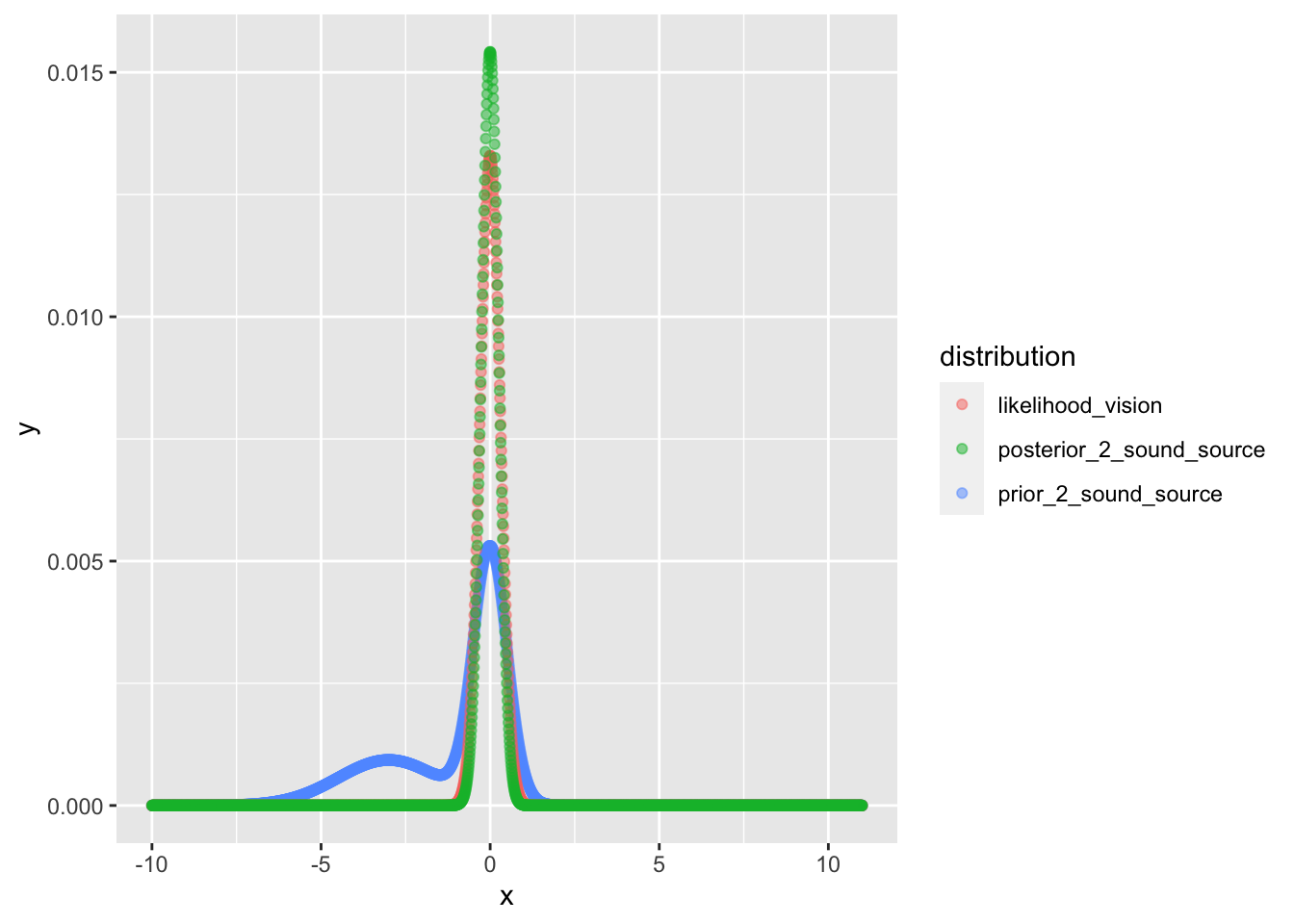
我们基本上能看到最终的结果, 在橙色的似然分布影响下, 我们得到的最终后验结果基本上仍然是一个均值为 0 的正态分布, 也就可以理解为, 在视觉信息的强作用下, 即使有很大的干扰, 我们仍然会产生屏幕上的人在说话的知觉——而且很确信.

2.4 大脑编码模型

我们刚才遇到的例子, 都是已经假定了先验分布和似然, 求解后验函数. 但实际上在我们的研究中, 这个过程可能需要倒推过来. 让我们看看下面的这张示意图:

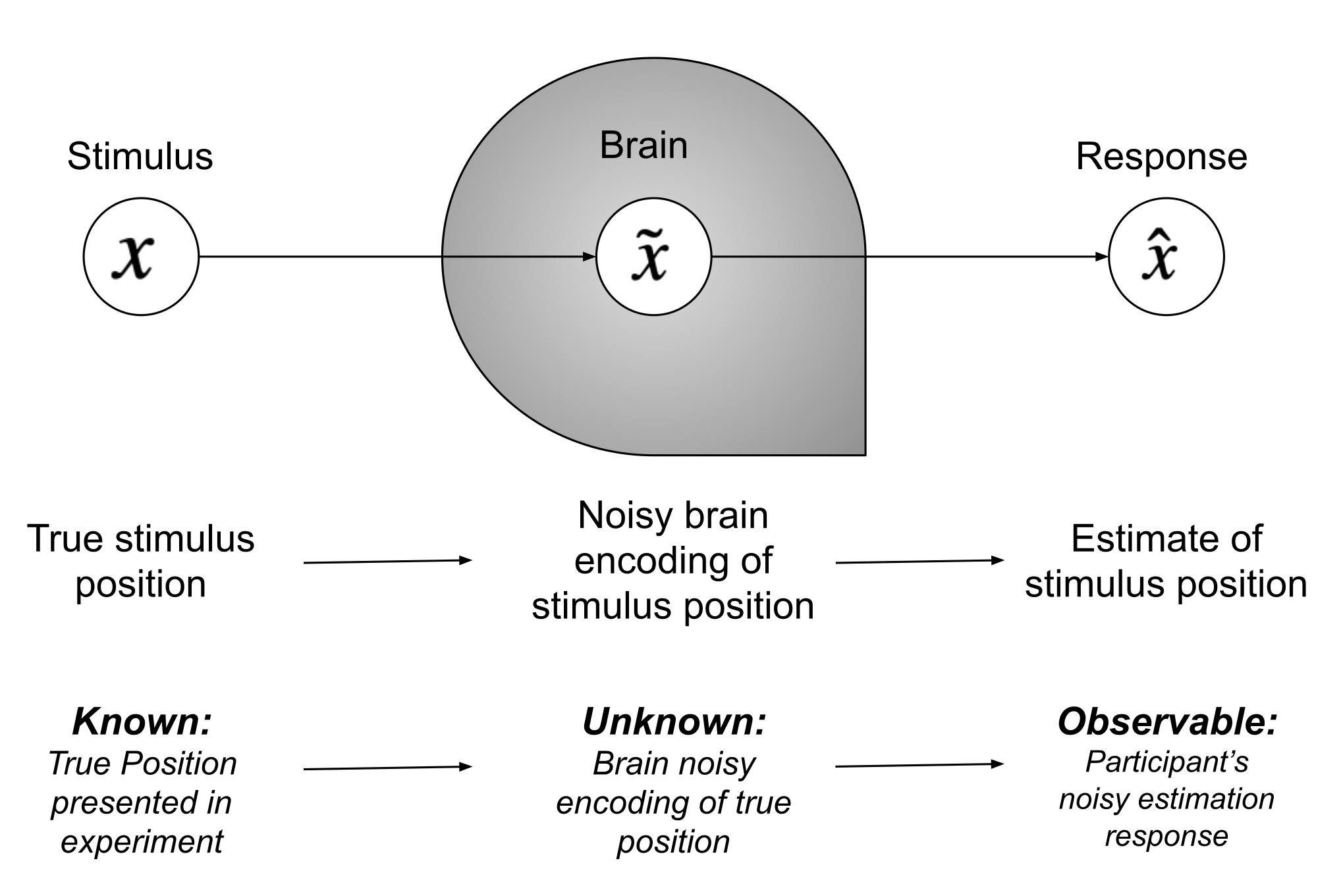
在我们的研究当中, 我们通常只能知道被试所感知事物的物理特性, 同时也可以通过测量被试的行为从而知道观测的结果, 但是中间的编码过程我们并不知晓. 但是我们可以借助贝叶斯工具来对这个过程进行建模:

1. 表征被试需要认识的外部特征作为先验 \(x\)
2. 大脑存在有噪声的对其他线索的认识, 可以表征为 \(p(\tilde{x} \mid x)\)
3. 大脑将其他线索的认识 (似然) 与先验整合起来, 得到后验 \(p(x \mid \tilde{x})\)
4. 大脑根据后验信息作出反应 \(\hat{x}\)

为了避免歧义, 我们把刚才的例子代入: 我们为了确认声源的位置, 大脑首先表征了先验, 随后将视觉信息作为似然进行信息更新, 最终得到的后验结果便为我们认为声源的位置, 并据此进行推断声源确实是屏幕上演员的面孔附近.

接下来让我们一步步对这个认知过程进行建模.

2.4.1 构建似然数组

这次, 为了让我们的模型成为一个更加普适的模型, 我们会将大脑的潜在的每种可能编码都绘制出来. 因此我们会创建一个多重似然函数 \(f(x) = p(\hat{x} \mid x)\) , 并且在一个平面上将这个函数进行可视化: x 轴对应 x 值, y轴对应 \(\hat{x}\) .

我们同样使用之前的 my_gaussian() 函数. 为了构建我们的数组, 将进行以下步骤:

1. 根据不同的均值创建不同的 \(\sigma = 1\) 的一系列高斯分布.

2. 假设我们有1000个不同的均值, 那么我们会生成一系列不同的高斯似然分布.

3. 然后我们按照坐标将这一系列似然函数绘制出来.

x = seq(-8, 8, 0.1)
hypothetical_stim = seq(-8, 8, 0.1)

compute_likelihood_array <- function(x_points, stim_array, sigma=1){
  likelihood_array <- matrix(data = 0, nrow = length(stim_array), ncol = length(x_points))
  
  j = length(stim_array)
  for(i in stim_array){
    foo <- my_gaussian(x_points, i, sigma)
    #print(foo/sum(foo))
    likelihood_array[j, ] <- foo / sum(foo)
    j = j - 1
  }
  
  return(likelihood_array)
}

likelihood_array <- compute_likelihood_array(x, hypothetical_stim, sigma = 1)

让我们把上面的矩阵可视化:

matrix_coordinates_to_dataframe <- function(raw_matrix){
  row_count <- nrow(raw_matrix)
  col_count <- ncol(raw_matrix)
  
  output_dataframe <- as.data.frame(matrix(0, ncol = 3, nrow = row_count * col_count))
  colnames(output_dataframe) <- c("x", "y", "value")
  
  k = 1
  for(i in 1 : row_count){
    for(j in 1 : col_count){
      output_dataframe[k, 3] <- raw_matrix[i, j]
      output_dataframe[k, 1] <- row_count - i + 1
      output_dataframe[k, 2] <- j
      
      k = k + 1
    }
  }
  return(output_dataframe)
}

plot_bayesian_matrix <- function(matrix){
  matrix_coordinates_to_dataframe(matrix) %>% 
  ggplot() + geom_tile(aes(x = x, y = y, fill = value)) +
  labs(title = "Mulitlikelihood") + ylab("x_tilde") + scale_fill_continuous(type = "viridis")
}

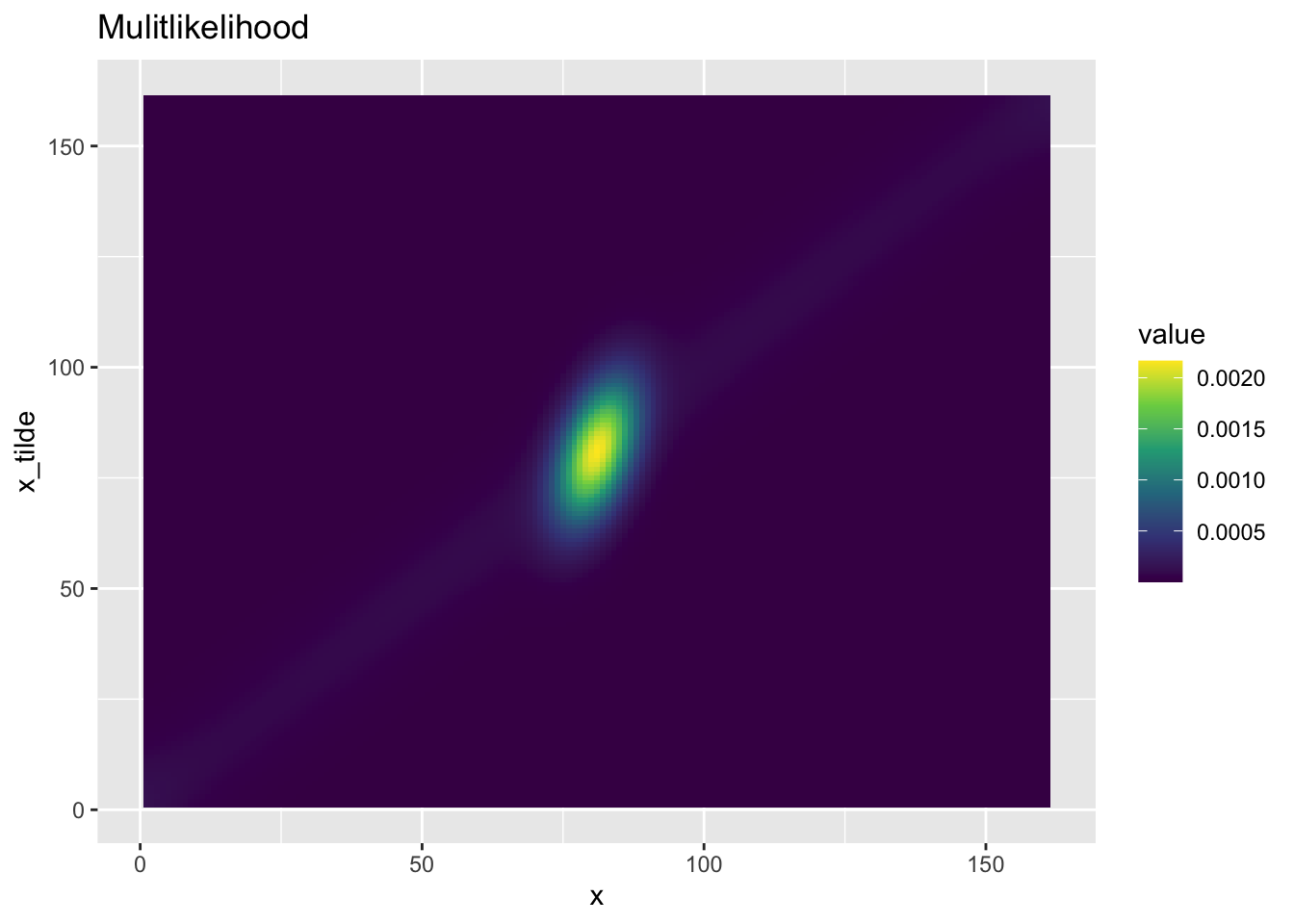
plot_bayesian_matrix(likelihood_array)

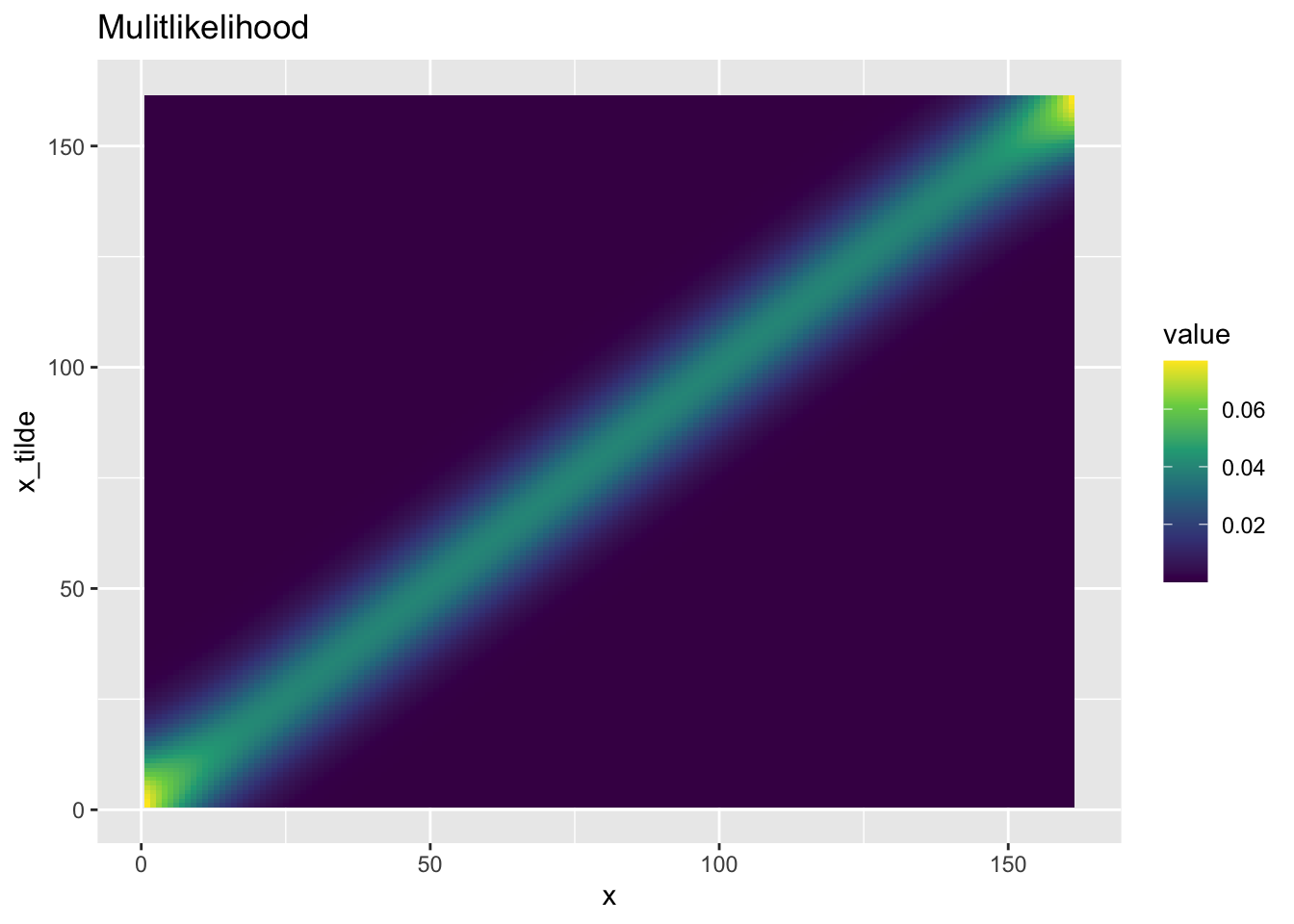
我们看到的这张图是由大量的高斯似然函数图像拼接起来的. 图中的颜色亮度越高, 代表了对应的点概率也就越高. 从图上我们可以看出来, 大脑所表征的空间位置 \(\tilde{x}\) 和真实的 \(x\) 接近的概率较大, 而其他范围则较小.

接下来让我们描述先验概率. 请注意, 在我们的模型当中, 大脑还未曾对外部信息作出的表征, 因此并不受外部信息的影响, 我们只需要描述真实概率分布 \(x\) 即可. 我们同样使用刚才的场景: 有 65% 的概率你听到的声音是从你正前方发出, 有 35% 的概率从另一边发出.让我们用代码实现这个模型.

calculate_prior_array <- function(x_points, stim_array,
                                  p_common,
                                  prior_mean_common = 0, prior_sigma_common = 0.5,
                                  prior_mean_indep = 0, prior_sigma_indep = 10){
  
  prior <- matrix(0, nrow = length(stim_array), ncol = length(x_points))
  
  col_idx <- length(x_points)
  
  for(i in stim_array){
    prior[, col_idx] <- mixture_prior(x_points, prior_mean_common, prior_sigma_common, prior_mean_indep, prior_sigma_indep, 
                                      p_1 = p_common)
    col_idx = col_idx - 1
  }
  
  return(prior)
}

prior_array <- calculate_prior_array(x, hypothetical_stim, 0.65) 
plot_bayesian_matrix(prior_array)

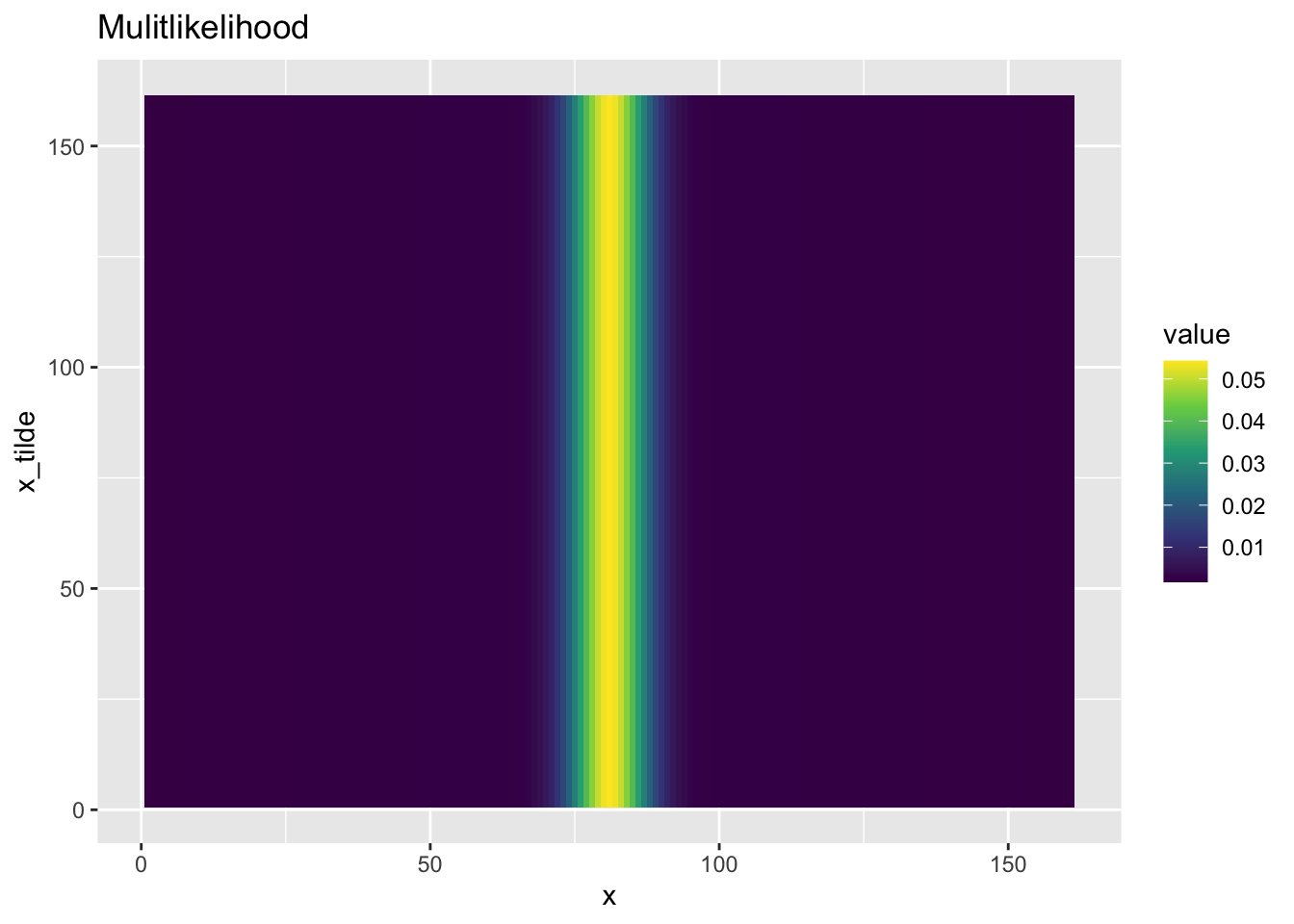
接下来我们需要计算后验分布. 你可能从前面的练习当中已经发现了, 由于我们关心的最终结果是点估计值, 这个值其实和具体的后验概率没有多大关系, 而与图形的形状息息相关. 因此, 我们可以完全不用在意贝叶斯公式右侧的分母, 只需用下面的公式来计算后验即可:

$$ Posterior[i,:] \propto$ Likelihood[i,:] \odot Prior [i,:] $$

上面的 \(\odot\) 符号代表矩阵点乘, 即矩阵各个对应元素相乘. 我们在前面已经构建出了大脑中的先验信息和似然函数, 我们使用点乘便可得到我们的后验数组:

posterior_array <- prior_array * likelihood_array / sum(prior_array * likelihood_array)
plot_bayesian_matrix(posterior_array)