表征相似性分析（RSA）快速入门教程

教程介绍

Ver. 0.1 beta

本教程翻译自 Mark A. Thornton 博士在宾大夏令营的 RSA tutorial 。为了便于理解，本文中夹带了大量补充信息，包括技术细节的解释和实验设计的描述，同时未于原文作明确区分，在此注明。

为了节省时间，存在大量的意译，且未推敲词句，仅保证尽可能高的准确性，并期望容易理解。

欢迎提交 issue 指出本文仍然没有解释清楚的地方，我会对本文持续迭代。

1. RSA 方法介绍

表征相似性分析（RSA）是一种基于二阶同构（second-order isomprhisms）的 fMRI 数据分析方法。这种方法并不是直接分析某个测量数据和另一个测量数据之间的关系，而是计算某个测量数据与其他数据之间的相似性，并进一步比较这些相似性数据。RSA 方法由 Kriegeskorte, Mur, and Bandettini (2008, Frontiers in System Neuroscience) 在 2008 年开创，并从此成为了分析神经成像数据的流行方法。本方法之所以能够变得非常流行，是因为RSA方法使用二阶同构进行分析，这种令人惊叹的分析技术可以将不同类型的脑成像、行为数据等研究数据联系起来。

在 fMRI 的分析过程中使用 RSA 方法，常常是需要在神经活动模式的相似性与任务、评分或者模型之间计算相关或者回归。在这个教程当中，我们会学习如何使用 RSA 进行验证性或探索性分析。

2. 如何测量相似性？

有很多种方法可以计算不同的数据对象之间的相似性（或者是差异距离）。虽然数据的本质会约束我们选择合适的方法，我们在线性空间当中衡量距离仍然有着很多种选择。这一节我们会讨论不同的距离度量，以使我们对最终作出的选择产生直观的感受。

对于fMRI数据，我们常常用来衡量相似性的是距离是平均距离、欧式距离和相关距离。本节我们会使用一些数据来模拟这些距离，展示这些不同的距离衡量方式之间的关系。

# 生成数据
set.seed(1)
sigmat <- matrix(c(1,0,.8,0,0,1,0,.8,.8,0,1,0,0,.8,0,1),nrow = 4) # 生成协方差矩阵

# 生成四组均值分别为（0，0，1，1），协方差为 sigmat 的随机数
dat <- mvrnorm(200, c(0,0,1,1), Sigma = sigmat) 

sigmat

##      [,1] [,2] [,3] [,4]
## [1,]  1.0  0.0  0.8  0.0
## [2,]  0.0  1.0  0.0  0.8
## [3,]  0.8  0.0  1.0  0.0
## [4,]  0.0  0.8  0.0  1.0

# sigmat 是生成数据的协方差
# 所以我们知道 1与3，2与4之间存在较高相关

# 绘制生成的随机数的图形
layout(matrix(1:4,2,2))
for (i in 1:4) {
  plot(dat[,i],type ="o",pch=20,ylim=c(-4,4),ylab="Activity",xlab=paste("Condition",as.character(i)))
}

我们在这里模拟生成的数据并不符合真实情况，但是它非常适合用来呈现本问题中三种不同距离度量的差异。你可以把这四个变量看作是在一个 fMRI 实验当中，四种不同的实验条件下大脑的 200 个体素的激活数据。

2.1 平均距离（均值差异）

我们将首先开始计算平均距离 - 仅仅是这四种条件的均值的差异。这种测量方式会舍弃体素之间模式的全部信息，而且非常类似于标准的单变量 fMRI 分析。下方的棒状图和热图反映了这个均值差异。

# 平均距离 mean distance

# 计算每个变量（数据对象）的平均值
# 每列代表一个变量（实验条件）下的数据，apply 函数使用参数 2 表示每个纵列
# 所以是对每个变量求均值

cmeans <- apply(dat,2,mean) 
barplot(cmeans) # 绘制均值

dmat1 <- as.matrix(dist(cmeans)) # calculate distance between means
levelplot(dmat1) # heatmap of distances

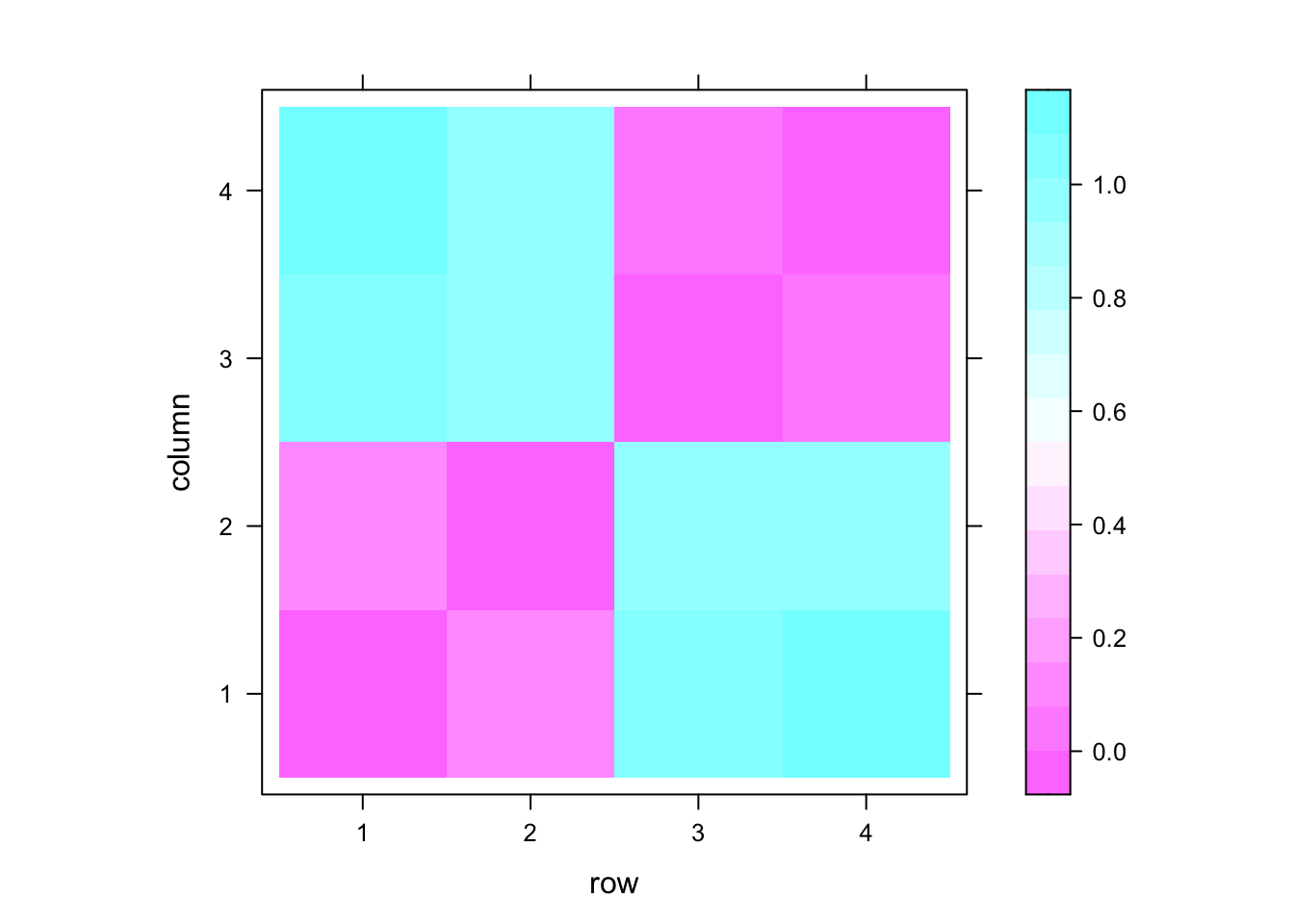
我们还记得我们刚才生成随机数的函数中的参数吧？其中第二个参数反映了生成变量的均值。因此我们可以看到第一第二变量的均值相近，第三第四变量的均值相近。故本图的含义很容易理解。

2.2 欧式距离

接下来我们将介绍欧式距离。欧式距离可以对应为我们常常在现实生活中所见到的“真实距离”。略微不同的是，相比于我们以前熟悉的在3维空间当中计算距离，在这里我们是要对N维空间的欧式距离进行计算。本例当中，N维空间的N是指 Voxel 的数量（即200个）。下面的热图和散点图反映了这四个条件的欧式距离。

# 欧式距离 Euclidean distance
dmat2 <- as.matrix(dist(t(dat)))
levelplot(dmat2)

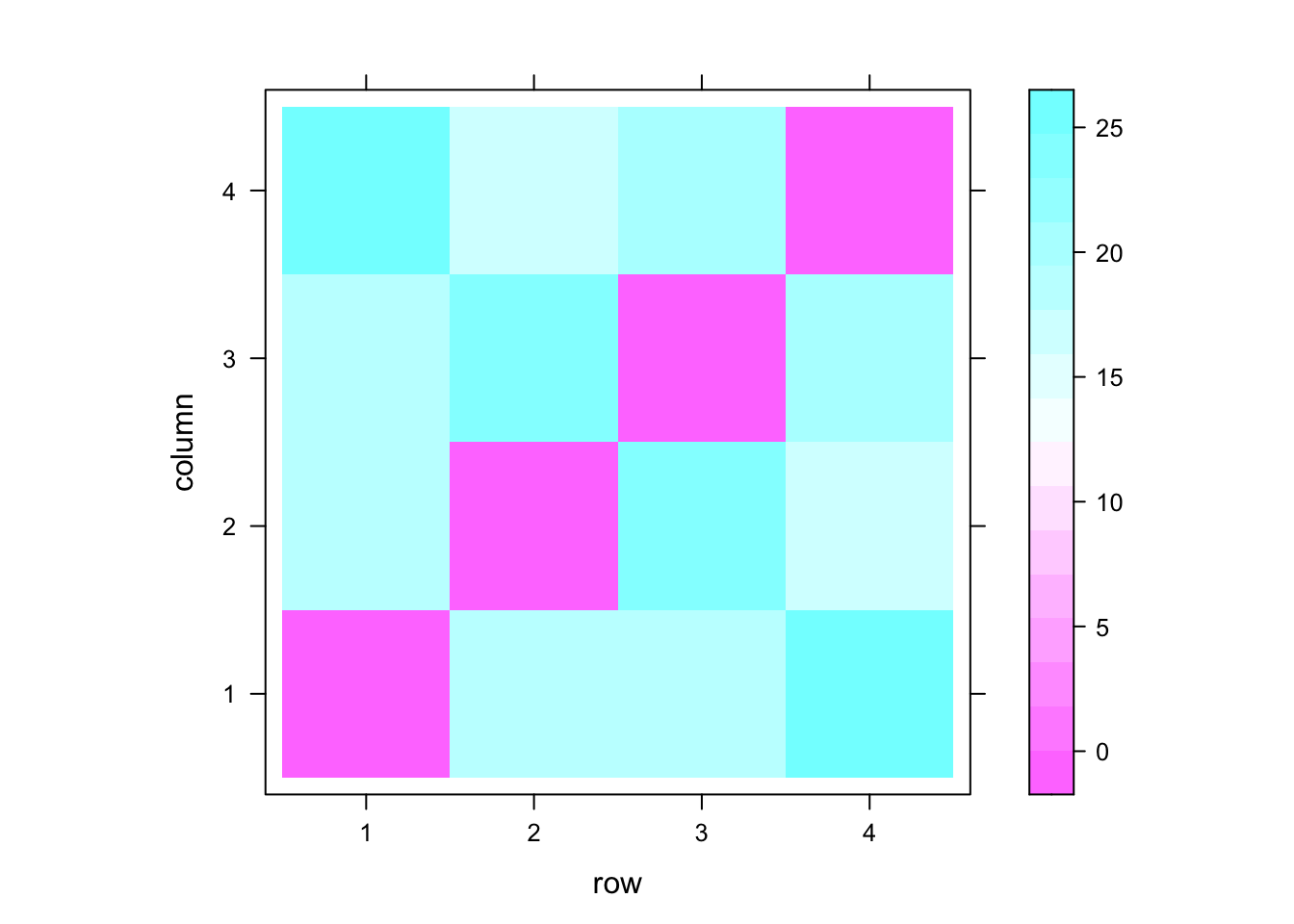
pairs(dat) # ？这样的 scatter plot 能反映距离吗？应该是在多维度上进行表征的才是距离。

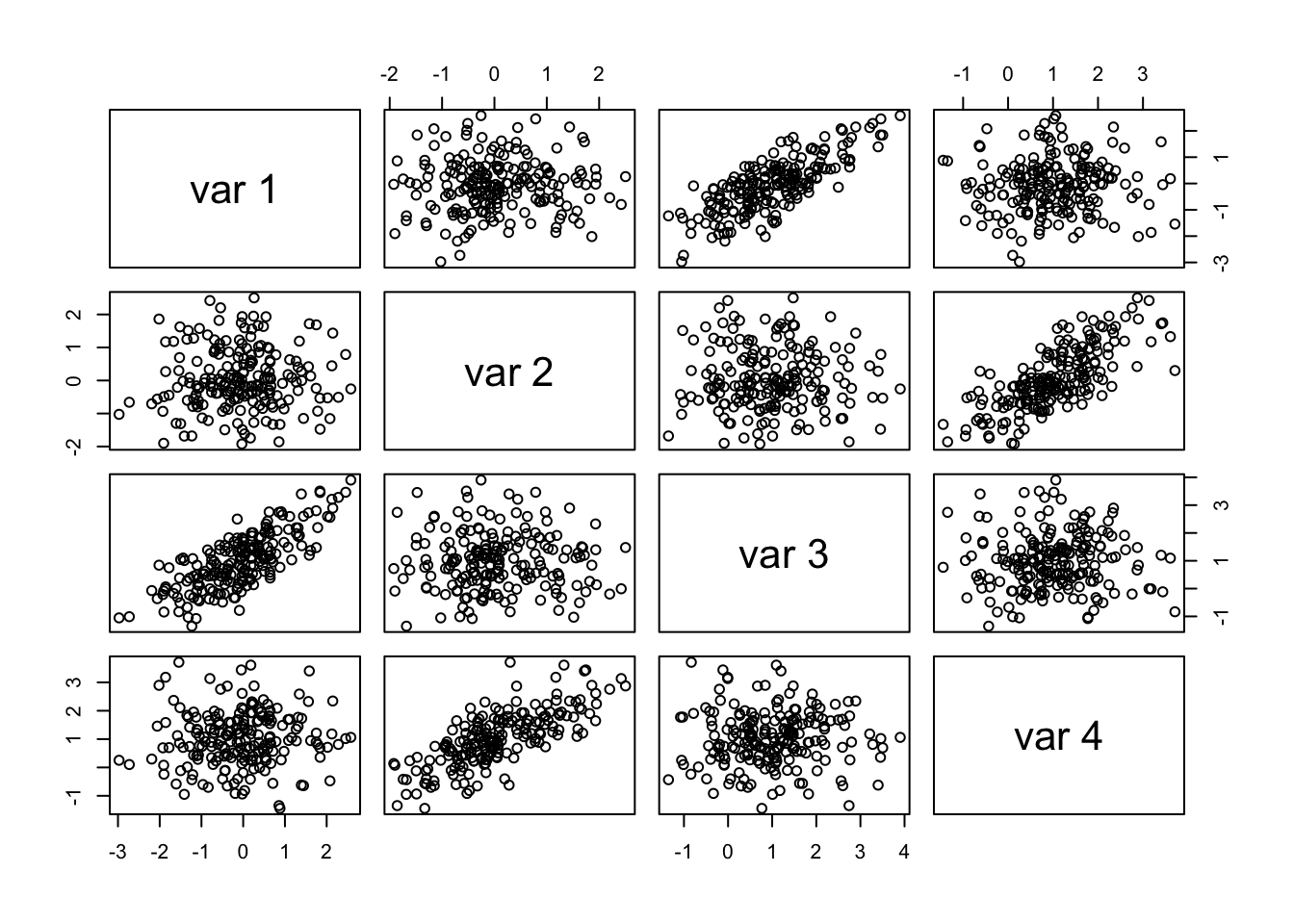
2.3 相关距离

相关距离可能是在 fMRI 分析当中最常用的距离了。这种距离完全舍弃了均值（数据在求相关时已经相当于进行了 z 分数化，否则的话那就是协方差分析了）。因为相关是用来描述相似性而非不一致性的，所以“距离”这个概念我们可以简单地把相关值“翻转”一下，用 1 - R 来表示。我们再次使用热图来描述这个结果。

# 相关距离 correlation distance
dmat3 <- 1 - cor(dat)
levelplot(dmat3)

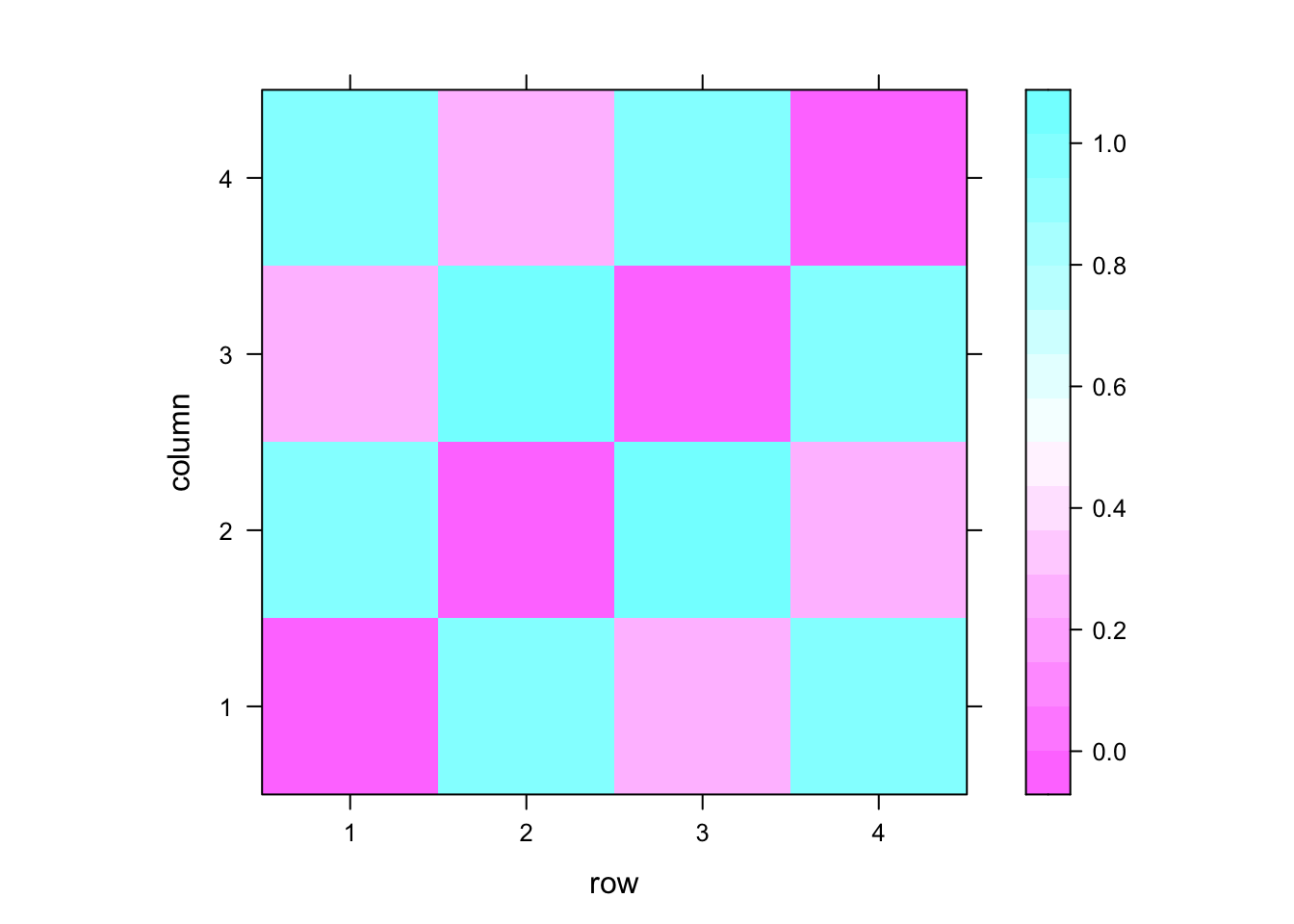
2.4 比较距离的测量方式

现在让我们来比较一下三种距离的测量方式。在下面的热图中，我们可以看到三者之间的关系：均值和相关距离之间完全无关，但是两者对欧氏距离有着贡献。相关距离可能是最佳的选择，因为在做 RSA 方法和一般的 MVPA 方法前，常常已经完成了多变量分析。因为多变量分析本身已经能够反映平均距离，所以在做 RSA 的时候，舍去均值信息是有意义的。然而，如果你只是正在对神经相似性进行简单的探索，同时对是均值还是模式导致差异并不太过关心，那么欧式距离也许是一个好的选择。

# combined plot
dmat2 <- dmat2/max(dmat2)
rlist <- list(raster(dmat1), raster(dmat2), raster(dmat3))
names(rlist) <- c("Mean","Euclidean","Correlation")
levelplot(stack(rlist),layout = c(3,1),at = seq(0,1,.01))

这个结果是否意味着使用相关来衡量神经相似性，可以使你的结果完全不受单变量分析方法的影响呢？很可惜并不是这样的。在这个简单的例子中，我们知道我们兴趣区的确切边界。然而在实际情况下，边界并不会这么清晰：激活模式与你选择的特征有关。举个例子来说，想象一下你的数据当中只有一个激活的团块，但是你的兴趣区非常的大，而这个团块只能填满这个兴趣区的 80%。剩下 20% 的体素在条件间则不会出现激活模式的改变。那么按照上面的方式进行分析，这两个体素群的差异同样会导致条件间相关性的存在——尽管在平均激活上是存在差异的。所以我再重申一下，单变量信息也许与你最后想要画的图没有关系，但是如果你的结论与非单变量分析的结果有着极强的联系，那么这对你来说也许不是一个好消息。

3. RSA方法：NHST，效应量，交叉验证，模型选择

本节我们会简单介绍 RSA 方法，并且围绕着它处理一些问题。特别是，我们将会演示如何在个体水平和组水平上检验 RSA 结果的意义。我们同样会了解到 RSA 的效应量方面的一系列的注意事项，同时学到如何进行交叉验证和模型选择。

不同与我们上面所做的那个像玩具一样的例子，本节我们会使用一个真正的 fMRI 研究数据。本数据来源于过去的一项研究。 Thornton & Mitchell, 2017, Cerebral Cortex

在本研究中，探讨 60 个社会名人的13项人格特质。研究涉及到的数据包括社会对这些名人的看法，被试对这些被试之间人格差异的比较，以及在想象这些名人时的脑功能活动数据。

社会对这些名人的普遍看法，将使用爬虫对维基百科的名人数据进行爬取，随后使用词袋法检索符合主题描述的词语。在名人之间的值两两求距离后得到本研究中的数据 holistic_dist$text 。

同样的，本研究请 869 人进行在线调查，对这 60 位名人在 13 个人格维度上进行了评分：warmth, competence, agency, experience, trustworthiness, dominance, openness to experience, conscientiousness, extraversion, agreeableness, neuroticism, attractiveness, and intelligence 。通过对这些评分之间求距离，得到了本研究当中的数据 holistic_dist$holistic

在脑成像研究中，参与者要求判断特定的陈述（例如“他想要学习空手道”）对特定人物（例如 Bill Nye）的适用程度。在整个研究过程中反复重复该过程，直到对 60 个目标在 12 个项目下进行评分。这些脑成像数据在预处理之后，使用 GLM 对相同目标人物在不同实验条件（目标任务）下的试次进行平均。在得到每个体素上的回归参数后，对参数进行 z 分数化来排除全局背景模式的影响，再在这些参数之间求相关。这是本例开始的地方。

我们可以看到上图当中，我们是选择性地选取了一些 ROI 作为后续分析的数据。这些 ROI 的选择的方法基于 Cronbach’s alpha 值。计算公式是 α ﹦（n / n -1）(1-∑Si2/St2) 。在本研究中，我们将阈值从 0 到最高值，按 0.01 进行划分，然后计算 Cronbach’s alpha 系数，找到最大的值便是我们的阈值。

首先，我们将会读取我们想要预测的神经模式的结果。这个数据由上图所示的体素当中的激活信号，经过 z 分数化后两两计算激活向量，得到相关值。

# 读取神经数据
neuro_data <- read.csv("https://raw.githubusercontent.com/dddd1007/MIND18_RSA_tutorial/master/neural_pattern_similarity.csv")
dim(neuro_data)

## [1] 1770   29

# 对数据按行取平均值
nsim <- rowMeans(scale(neuro_data))
length(nsim)

## [1] 1770

我们可以看到 neuro_data 变量的维度是 1770 * 29，其中 1770 是条件间的 beta 值之间的得到的相关值，29 是被试个数。

我们接下来则会载入一系列特征数据，是所有被试对名人在人格特质上进行的评分：

# 按维度读取信息
pdims <- read.csv("https://raw.githubusercontent.com/dddd1007/MIND18_RSA_tutorial/master/dimensions.csv")
pnames <- as.character(pdims$name)
pdims <- scale(pdims[,2:14])

rownames(pdims) <- pnames
levelplot(t(pdims),xlab="",ylab = "",scales = list(x = list(rot = 45)))

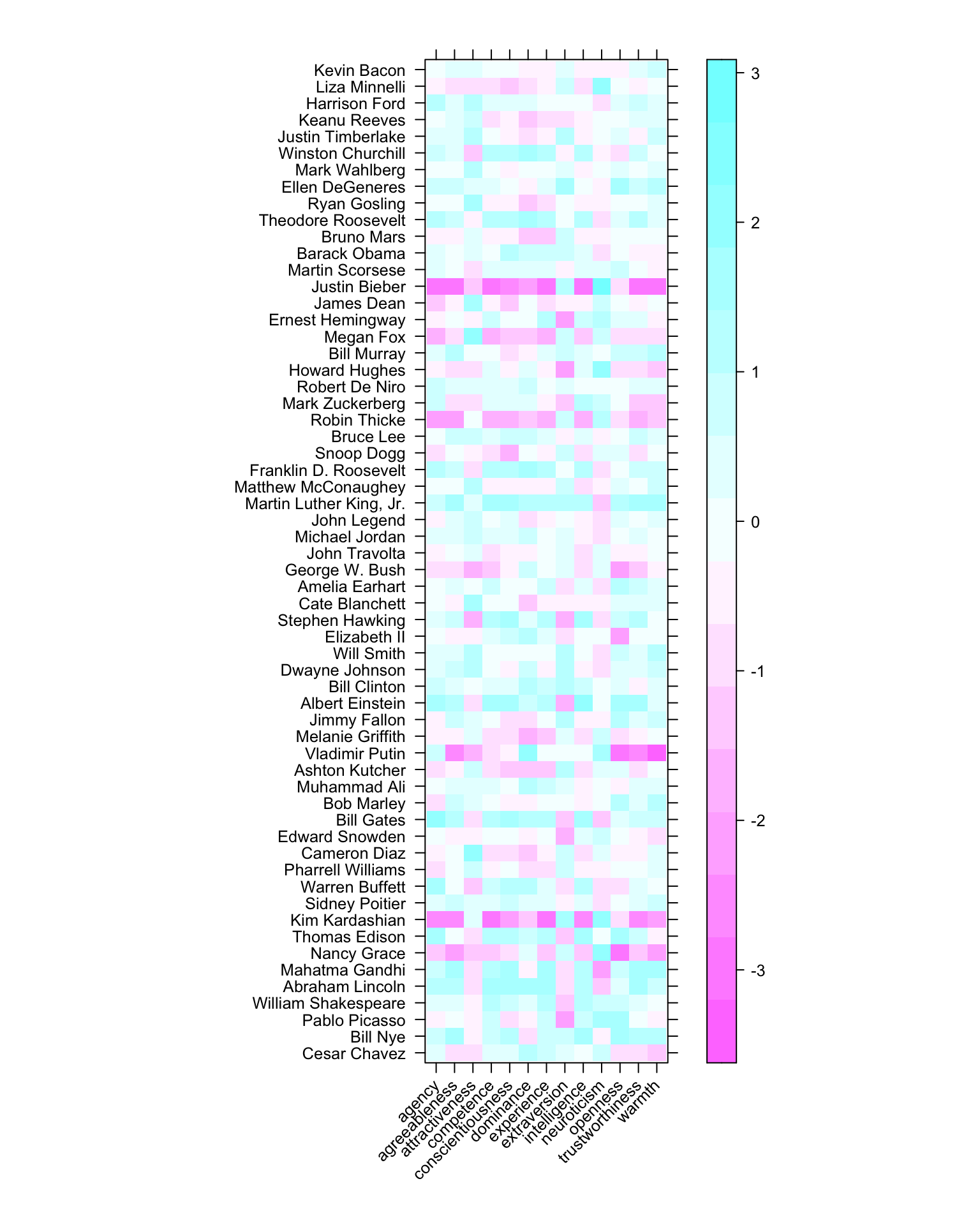
最终，我们将会读取一些整体的相似性测量信息：譬如在不同的目标名人之间的人格评分两两之间的距离，以及通过对这些伟人的维基百科页面进行词袋模型分析，来对文本信息相似性的评估。因为这些测量的形式都是反向编码（比如距离），因此我们会反转他们来得到这些信息的相似性。

我们读入的数据中，是对所有对名人之间两两比较得到的结果。故由1770个评分。$\left(\begin{array}{c}{60} \ {2}\end{array}\right)=\frac{60 !}{2 ! \times 58 !} = 1770$

holistic_dist <- read.csv("https://raw.githubusercontent.com/dddd1007/MIND18_RSA_tutorial/master/holdists.csv")
explicit <- 100 - holistic_dist$holistic
text <- 2 - holistic_dist$text

3.1 我们的第一个 RSA ！

现在我们已经在 R 当中载入了必要的数据，接下来让我们运行第一个 RSA 分析。这个分析将会对平均神经模式的相似性和对伟人的人格之间的相似性之间做一个相关。

cor(nsim,explicit)

## [1] 0.399468

plot(explicit,nsim,xlab = "Rated similarity",ylab = "Neural similarity",pch = 20)
abline(lm(nsim~explicit),col = "red",lwd = 2)

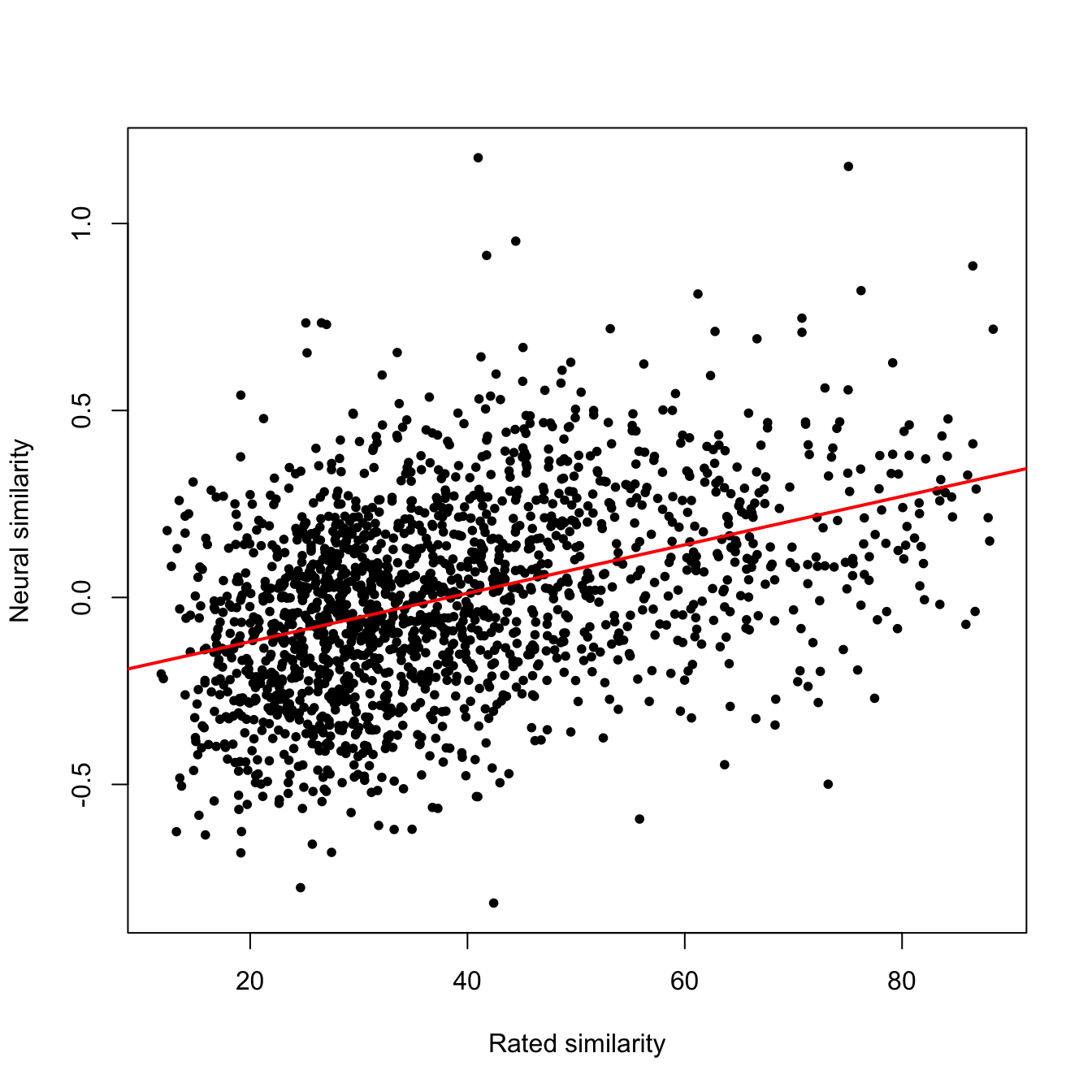
正如你所看到的，在人们想象那些名人如何看待其他人，与人们在想像这些人时的脑功能活动模式的差异之间，存在着明显的相关性。皮尔逊相关得到的 r 值为 0.4 。Kriegeskorte 和 Colleagues 建议使用斯皮尔曼相关来代替皮尔逊相关。他们的建议很有道理。但是我在实际的研究中，很少见到方法上的差异所导致的结果的不同。我们这里来尝试一下。

cor(nsim,explicit,method = "spearman")

## [1] 0.4039944

所以你能够看到，这就是表征相似性分析的基本概念。无论是脑成像的结果，还是评分的结果，这两者都是对实验中刺激（60位伟人）的特征描述。虽然这样的特征之间我们没有办法直接进行比较，但是将他们之间两两计算距离之后，我们得到的信息是“两个伟人之间的差异”。而这种差异在表征上具有一致性，即虽然原始信息不一样，但是他们的二阶数据上是同构的，因此我们基于二阶同构，对新的数据可以比较其相似性。

Null hypothesis significance testing

我们如何判断这个相关是否统计显著呢？做一个独立样本相关参数检验能够给我们一个固定效应的 p 值。

cor.test(nsim,explicit)

## 
## 	Pearson's product-moment correlation
## 
## data:  nsim and explicit
## t = 18.322, df = 1768, p-value < 2.2e-16
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  0.3595679 0.4379099
## sample estimates:
##      cor 
## 0.399468

我们能够看到检验的结果非常的显著。然而，如果我们的模拟练习仅仅是从大量数据当中获取的一个小样本，我们也许希望结果是一个能够反映相似性矩阵依赖性的 p 值。为了实现这一目标，我们可以使用置换检验。正如我们平常使用的置换检验一样，在独立样本水平上进行置换十分重要。在本例当中，这意味着我们需要对不同的相似性矩阵之间的行列之间进行互换。

# 将向量化的神经元相似性矩阵转换回矩阵
sqnsim <- squareform(nsim)

# 为可重复性分析设置随机数
set.seed(1)
nperm <- 5000 # 设置置换次数
nppl <- dim(sqnsim)[1] # 实验中的刺激物（伟人）个数
permcor <- rep(NA,nperm) # 定义变量
for (i in 1:nperm){
  sel <- sample(nppl) # 置换向量（选择第几行/第几个伟人）
  rnsim <- squareform(sqnsim[sel,sel]) # 置换矩阵并重新向量化
  permcor[i] <- cor(rnsim,explicit)    # 重新计算相似性
}

# 重新计算相似性的p值
mean(abs(permcor) > cor(nsim,explicit))

## [1] 0

# 对p值的结果进行可视化
hist(abs(permcor),xlim=c(0,.4),main="Permuted null versus actual correlation")
abline(v=cor(nsim,explicit),col="red",lwd=2)

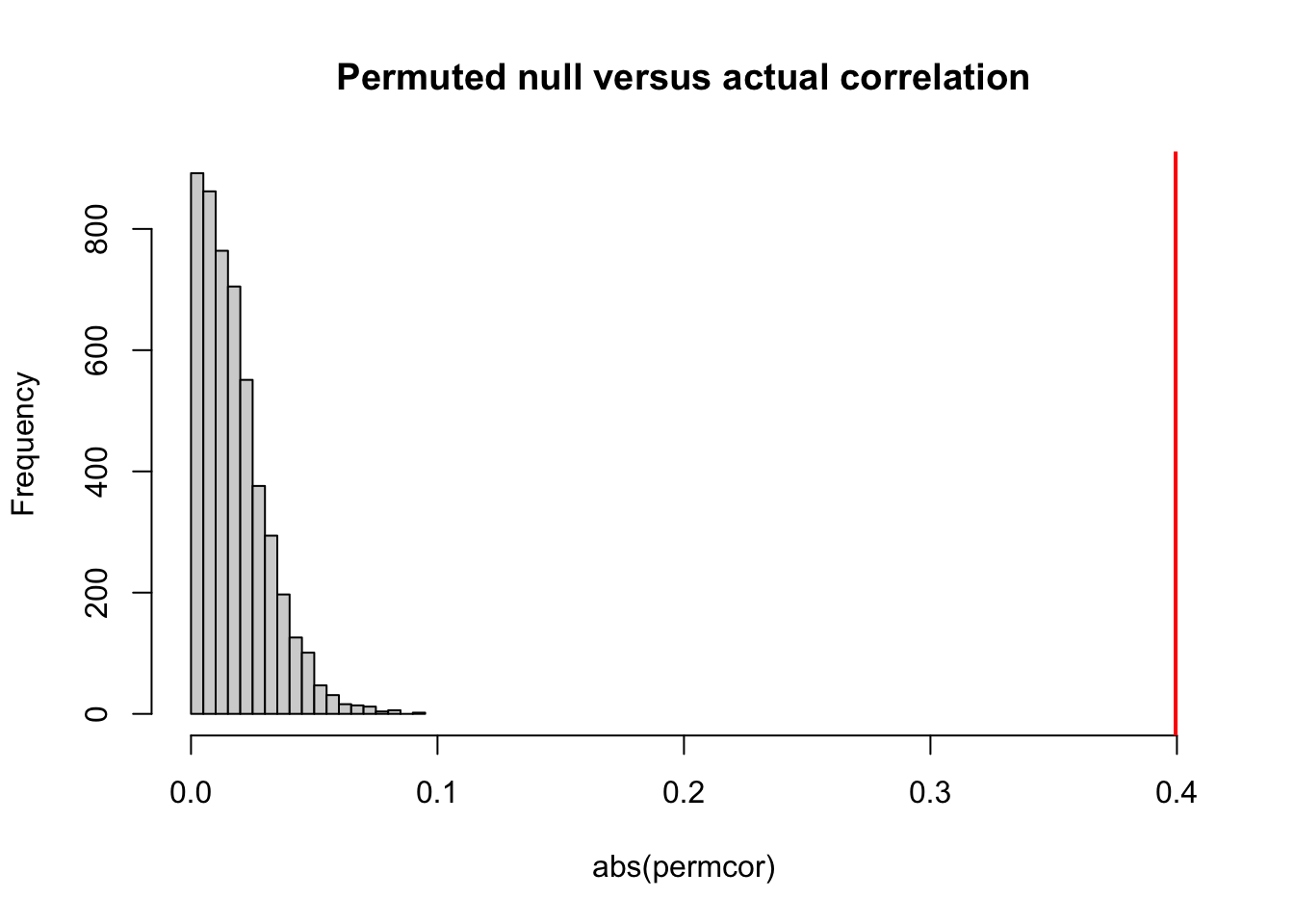
正如你所看到的，在本例当中，我们的置换检验结果显示，p值大部分仍然保持在0左右。但是请记住的是大多数情况并不和本例一样。

置换检验解决了结果是否依赖于相似性矩阵的形态这一问题，但是我们所做的相关性分析仍然在只在项目水平上是有效的（因为我们在不同的被试间平均了神经相似性）。因此，我们获取的p值严格来说是对被试样本的推断，而是对实验中呈现的名人的样本的推断。为了得到更一般的对应于社会群体的结果，我们需要进行一个随机效应分析。最简单的方法是进行一个摘要分析。

# 对每一个被试进行相关分析
ncors <- cor(explicit,neuro_data)

# 对参数进行单个样本t检验 (注意求一个双曲函数)
t.test(atanh(ncors))

## 
## 	One Sample t-test
## 
## data:  atanh(ncors)
## t = 11.624, df = 28, p-value = 3.144e-12
## alternative hypothesis: true mean is not equal to 0
## 95 percent confidence interval:
##  0.08572848 0.12240606
## sample estimates:
## mean of x 
## 0.1040673

在上面的例子中，我们对每个被试的神经相似性和伟人的比较评分之间求了相关。随后我们对结果做了一个单样本t检验，来判断均值是否大于零。注意这个时候算出的相关值是非线性且不服从正态分布的，所以我们通过费舍尔 z 转换使得相关值符合参数检验的先验条件。如果通过转换也没有办法获得一个符合 NHST 前提的数据，我们同样可以像下面一样通过 bootstrapping 方法做非参数检验。

# bootstrap 95% CI
bootres <- replicate(5000,mean(sample(ncors,length(ncors),T)))
quantile(bootres,c(.025,.975))

##       2.5%      97.5% 
## 0.08668102 0.12000557

# visualize result
plot(1:29,sort(ncors),xlab="Participant (sorted)",ylab="Correlation (r)",
     pch=20,xlim=c(1,30))
points(30,mean(ncors),col="red",cex=2,pch=20)
segments(30,quantile(bootres,.975),30,quantile(bootres,.025),col="red",lwd=2)
abline(h=0)

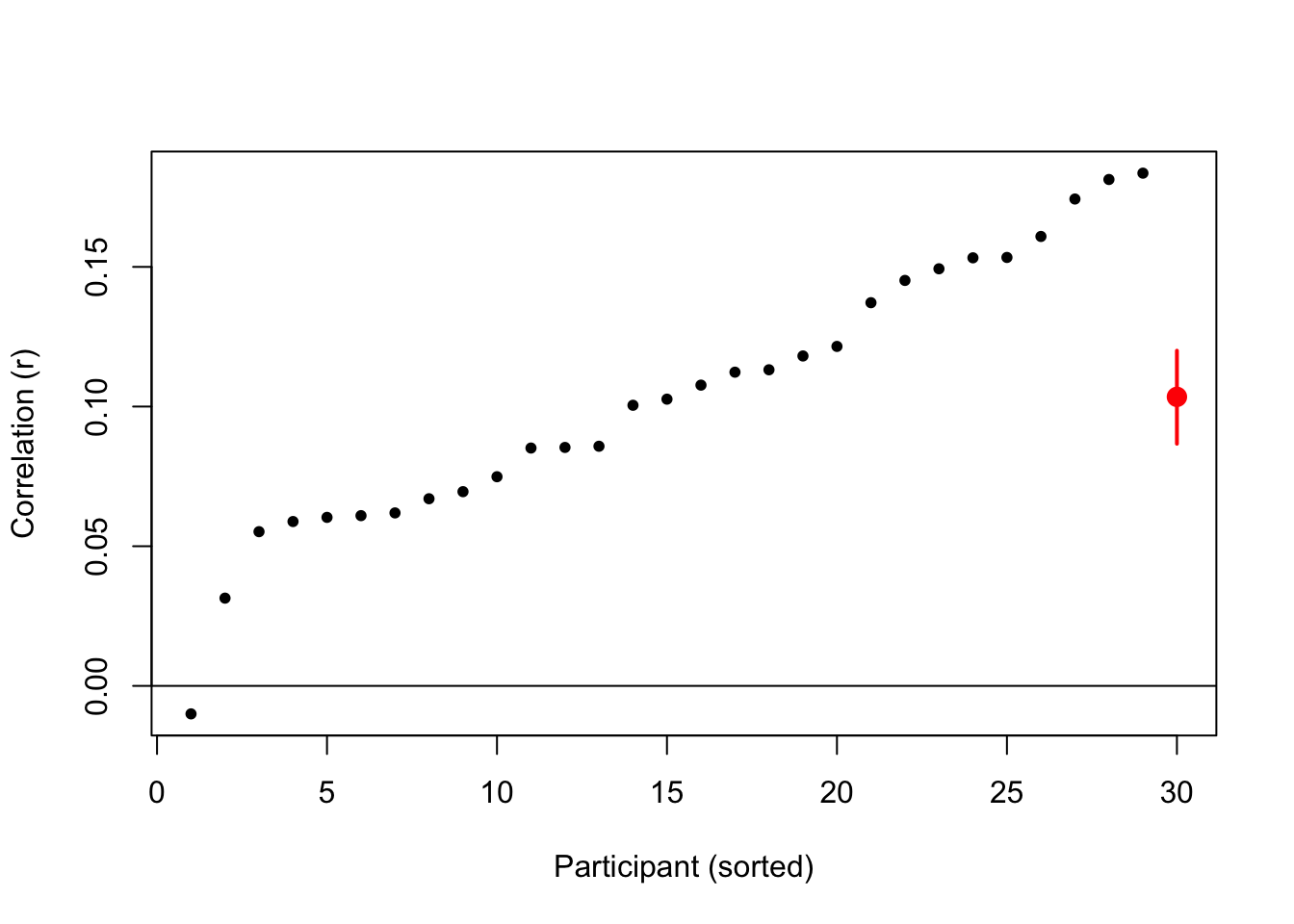
注意几乎所有的相关值都大于0，只有一个被试的相关值是小于0的，因此 NHST 无需拒绝零假设。

尽管在组水平上分析数据能够让我们来推断总体，但是最佳的 NHST 方法应该能让我们对被试和项目层面都能进行随机效应分析（对所有对自变量的随机截距和随机斜率都进行分析）。然而不幸的是，由于相似性矩阵的随机效应结构的复杂性，最佳的最大随机效应模型非常难以收敛。因此对于大多数的 RSA 分析来说，几乎不可能得到最为正确的 NHST 结果。然而还有一些备选方案，比如 感染率推断 。另一种选择是使用贝叶斯统计，因为贝叶斯混合效应模型有时能够收敛最小二乘法无法收敛的模型。这些选择已经超出了本教程所要介绍的范围，但是后面我们会谈一下另一种解决这个问题的方式：交叉验证。

3.2 效应量

效应量在 RSA 中相对比较简单直接。就像我们之前所做的，在项目水平上的分析，效应量就是两个相似性测量变量之间的相关而已。然而，当你做这个分析的时候，考虑你的测量数据的信度仍然是一件有意义的事情。神经测量数据往往混杂有大量的噪声，这常常会导致它与其他测量数据之间计算相似性的时候，得到的结果比真实情况更小。解决这个问题的其中一种办法是衰减校正，即在分析中消除测量误差对相关结果的衰减作用（Jensen，1998）：

# 计算原始相关系数
cor(nsim,explicit)

## [1] 0.399468

# 计算成像数据中被试间的 Cronbach alpha 系数
rel <- alpha(neuro_data)

## Warning in alpha(neuro_data): Some items were negatively correlated with the total scale and probably 
## should be reversed.  
## To do this, run the function again with the 'check.keys=TRUE' option

## Some items ( V13 ) were negatively correlated with the total scale and 
## probably should be reversed.  
## To do this, run the function again with the 'check.keys=TRUE' option

# 呈现标准化alpha系数
rel$total$std.alpha

## [1] 0.5033655

# 校正相关衰减
cor(nsim,explicit)/sqrt(rel$total$std.alpha)

## [1] 0.5630413

我们的计算当中涉及到科隆巴赫 α 系数，这是在心理测量学中最常用的信度评估信度工具，用以检验测量工具的内部一致性。该值越高则表明测量工具有着较高的内部一致性，测量工具的信度也就越高。在这里衡量的就是我们的脑成像测量结果的稳健性。

在本例当中，当我们校正了神经测量数据的糟糕的信度，神经元和外显比较分数之间的的相关从 0.4 增长到 0.56 。如果我们用被试个体数据来计算其信度，则可以对评级分数进行相同的计算。注意只有原始相关系数能够用于 NHST 分析。同样需要记得的是我们在这里计算的数据的信度仅仅是数据的变异性。当估计数据本身就是充满噪声的（比如小样本数据），那么必定得到较差的结果。因此，尽管这种方法是有效的，然而在应用的时候仍需注意。

除了测量信度的问题外，还有另一个原因可能导致 RSA 计算得到的相关小于他们真实的结果：将原始数据转换为相似性矩阵会导致信息量的衰减。平均来说， RSA 分析得到的相关度将会是背后多维度数据相关度的平方根。

如果你关心表征相似性中差异性的解释本身，那这些并不是一个重要的问题。但是如果你关心的是在相似性背后那些变量的变异性，那么你可以通过对你做的 RSA 相关取平方根来估计你的效应量。

3.2.1 组水平的效应量

在组水平上，我们可以通过计算 Cohen’s d 值来计算效应量。

# 计算 Cohen's d
mean(atanh(ncors))/sd(atanh(ncors))

## [1] 2.158543

在这个例子中，我们能够看到总体评分和神经活动的相似性之间的 Cohen’s d 值是 2.16. 根据标准，当 Cohen’s d 值大于 0.8 时，我们可以说“大效应量”。我们得到的是这个值的 2.5 倍，因此我们得到了一个巨巨大的效应量。

在基于多元回归或混合效应模型的 RSA 中，还可以估计广泛的其他标准化效应量。但是，这些措施不是仅对应于 RSA 的，所以在这里不予考虑。

3.3 交叉验证 Cross-validation

显著性检验能够提供对总体数据的推断可靠的验证。然而，交叉验证方法能能够提供更稳健的方法来评估你的模型在多大程度上能够对你的数据进行预测。在交叉验证中，我们会使用一部分数据训练一个模型，随后用剩下对数据来进行检验，重复这个过程对数据对子集反复进行训练和检验。让我们来进行一个基于交叉验证对多重回归 RSA，计算总体评价和文本信息，对于神经表征的相似性。

# 配对绘制项目水平上的散点图
pairs(data.frame(neural = nsim,explicit,text),pch = 20)

# 对神经测量数据进行标准化，使得所有值均为正值
neuro_datap <- neuro_data - min(neuro_data)

# 进行留一交叉验证

# 使用整体评分和文本分数定义一个矩阵，后面使用非负最小二乘法求解，这里的1相当于定义截距
xvars <- cbind(1,explicit,text)
nsub <- dim(neuro_data)[2]
cvperf <- rep(NA,nsub) # 定义迭代中计算得到的相关性结果变量
for (i in 1:nsub) {
  fit <- nnls(xvars,rowMeans(neuro_datap[,-i])) # 使用非负最小二乘法估计
  # nnls 函数使用 Lawson-Hanson NNLS 方法，计算 neuro_data[， -1] 在 xvars 上的投影 fit$fitted
  # fit$fitted相当于除去了噪声的最佳估计值
  cvperf[i] <- cor(fit$fitted,neuro_datap[,i])
}
mean(cvperf)

## [1] 0.1109283

我们在这里可以看到，这两个预测变量在做交叉验证后，得到的模型性能结果 r 为 0.11. 注意这时我们可以有很多变量来描述模型性能，例如均方根误差 RMSE 等等，但是相关值是相当容易被解释的。然而，我们如何解释这个模型性能呢？r = 0.11 明显看起来不是一个很好的结果，但是我们能得到的最好的结果是怎样的呢？我们可以通过计算一个噪声上限来回答这个问题。噪声上限（noise ceiling）是指预测变量能够解释的最大程度。在这个情境下，噪声上限是每个个体和其他个体的平均值之间的相关。（小夏注：这个概念称为 noise ceiling 我感觉容易误导，如果称为 predict ceiling 也许更好一些）。

noise <- rep(NA,nsub)
for (i in 1:nsub){
  noise[i] <- cor(neuro_data[,i],rowMeans(neuro_data[,-i]))
}
mean(noise) # noise ceiling

## [1] 0.1293295

mean(cvperf)/mean(noise) # 对噪声上限的解释度

## [1] 0.8577185

本数据的噪声上限只有 0.129，这意味着在给定的被试间差异性当中，理论上最佳模型的解释度不会超过 0.129. 如果将我们做交叉验证得到的结果和噪声上限相除，我们能够看到，这两个变量能够达到最佳模型 86% 的解释度。虽然在计算方法上有些不同，但你可能会意识到我们刚刚所做的交叉验证在概念上与我们之前执行的相关性衰减相同。因此，尽管噪声上限对理解我们对结果可能有所帮助，但是我们仍然需要对它抱有怀疑，因为它们只是估计值，并且有着前提假设假设。例如，在上面的例子中，我们存在一个潜在假设，所有有意义的变异都在组水平上（我们把被试的神经测量信号平均了），这几乎是不可能的。

从更一般的角度来讲，使用不同的交叉验证方法对估计数据当中不同的“边界”的泛化非常有用。在如上的例子当中，我们只能对被试进行交叉验证，但是在下面的例子中，我们同样可以对心理状态进行交叉验证。

# 定义函数用于转换备选向量为矩阵，并重新转换为向量（需要结合下方代码理解）
rsasel <- function(selvec){
  nobj <- length(selvec)
  selmat <- matrix(F,nobj,nobj)
  selmat[selvec,selvec] <- T
  diag(selmat)<-0
  return(squareform(selmat))
}

# 依据刺激物分割数据到训练集与测试集
set.seed(1)
targsel <- sample(c(rep(T,30),rep(F,30)))
targsel1 <- rsasel(targsel)==1
targsel2 <- rsasel(!targsel)==1
neuro_datap1 <- neuro_datap[targsel1,]
neuro_datap2 <- neuro_datap[targsel2,]
xvars <- cbind(1,explicit,text)
xvars1 <- xvars[targsel1,]
xvars2 <- xvars[targsel2,]
  
  
# 进行被试留一验证和刺激物分半验证
nsub <- dim(neuro_data)[2]
cvperf <- matrix(NA,nsub,2)
for (i in 1:nsub){
  fit <- nnls(xvars1,rowMeans(neuro_datap1[,-i]))
  cvperf[i,1] <- cor(xvars2 %*% fit$x,neuro_datap2[,i])
  fit <- nnls(xvars2,rowMeans(neuro_datap2[,-i]))
  cvperf[i,2] <- cor(xvars1 %*% fit$x,neuro_datap1[,i])
}
mean(cvperf)

## [1] 0.1028134

当我们尝试将这种方法推广到对刺激物进行分组时，模型的性能表现比起之前的 0.111 降到了 0.108. 然而，这对模型性能的负面影响只有一点点，提示这个模型可能对新的目标人物具有较好的泛化效果。在实践中，我们可能需要以不同分组（或其他的交叉验证方法）反复重复上述过程，从而确保我们得到较好的结果并非侥幸。注意交叉验证方法能够给我们以显著性检验很难提供的答案，正如我们前面所提到的，使用显著性检验很难在分析混合效应模型的时候得到收敛结果。

3.4 模型选择

到目前为止，我们已经分析了预测变量为一个到两个的模型。在很多的研究当中，研究者会尝试在很多维度上解释神经相似性。当建模变得越来越复杂时，我们何时可以说我们已经构建解释脑功能活动最佳的 RSA 模型？模型选择虽然不是仅限于 RSA 方法中的问题，但却是非常重要的。为一个回归模型选择最佳的特征集合有很多种好方法。传统的方法包括逐步回归和最优回归子集法。然而，这里我们给出一个从较小的特征集合当中进行简单穷举搜索的例子。

我们请被试对这些名人进行评分时所得到对诸多预测变量之上，有着大五人格这个基本维度，即开放性（openness），责任心（conscientiousness，外倾性（extroversion），宜人性（agreeableness），神经质性（neuroticism）等。如何对这些预测变量进行组合，最能够解释我们对这些名人的神经表征的模式相似性呢？

# 选择评价矩阵当中最合适的维度
big5 <- pdims[,c(2,5,8,10,11)]
big5d <- -apply(big5,2,dist) # 转换为距离
big5d <- big5d - min(big5d) # 确保数值都为正

# 列举所有可能的组合
b5combs <- list()
ind <- 1
for (i in 1:5){
  ccombs <- combn(5,i)
  for (j in 1:dim(ccombs)[2]){
    b5combs[[ind]] <- ccombs[,j]
    ind <- ind + 1
  }
}

# 对所有的组合拟合模型进行计算
nc <- length(b5combs)
perf <- matrix(NA,nc,nsub)
for (i in 1:nc){
  xvars <- cbind(1,big5d[,b5combs[[i]]])
  for (j in 1:nsub){
    fit <- nnls(xvars,rowMeans(neuro_datap[,-j])) # fit using non-negative least squares
    perf[i,j] <- cor(fit$fitted,neuro_datap[,j])
  }
}
# 标记表现最佳的模型
mperf <- rowMeans(perf)
colnames(big5)[b5combs[[which(mperf==max(mperf))[1]]]]

## [1] "conscientiousness" "extraversion"      "neuroticism"      
## [4] "openness"

我们看到最佳的模型是将大五人格当中的四个因素组合起来：责任心，外向性，神经质，开放性。在实践当中，如果我们想要继续估计这个模型的表现（比如计算一下噪声上限），我们最好分离模型选择和估计模型效力的步骤。在这个研究中，我们只检测了31中可能的模型（大五人格的排列组合），但是可以选择模型的空间会随着备选的预测变量的增加而迅速地增长。这意味着只要稍微多一点点维度，我们就会在模型选择上遇到极大的过拟合风险。使用独立数据进行模型选择和评估可减少这种风险。

4. 数据探索和可视化

到目前为止，我们主要从验证的角度考察了表征相似性方法：尝试使用模型拟合测量的神经数据。但是，探索性分析（包括可视化）有着至关重要的补充作用。在本节中，我们将探究几种重要的探索性方法和可视化技术。

4.1 多维缩放法（Multidimensional Scaling, MDS）

多维缩放法是一种非常强大的对数据相似性进行探索和可视化的技术，属于流形学习的一种。

流型学习可以理解为是一种降维方法。流形学习的视角下，我们在高维空间当中表征的数据都是低维空间当中的映射。因此我们可以在保持低维空间形状的前提下对高维数据进行描述。比如二维图形中的圆，我们可以使用单一特征值半径来进行描述，则即保留了圆的特征，又能对数据进行降维。这种方法的基本思想就是将距离矩阵中的点的构型进行重构，使得这些点的距离尽可能准确地表征在N维空间当中。在实践当中，这里的N通常为 2 （或者3），因为这样可以使得结果容易可视化。在 R 当中有大量的包可以使用，我们在这里使用的是 smacof 包。

一个简单示例：法国城市的航线距离

layout(mat=matrix(1))
mdfit <- smacofSym(Guerry,2)
plot(mdfit) 

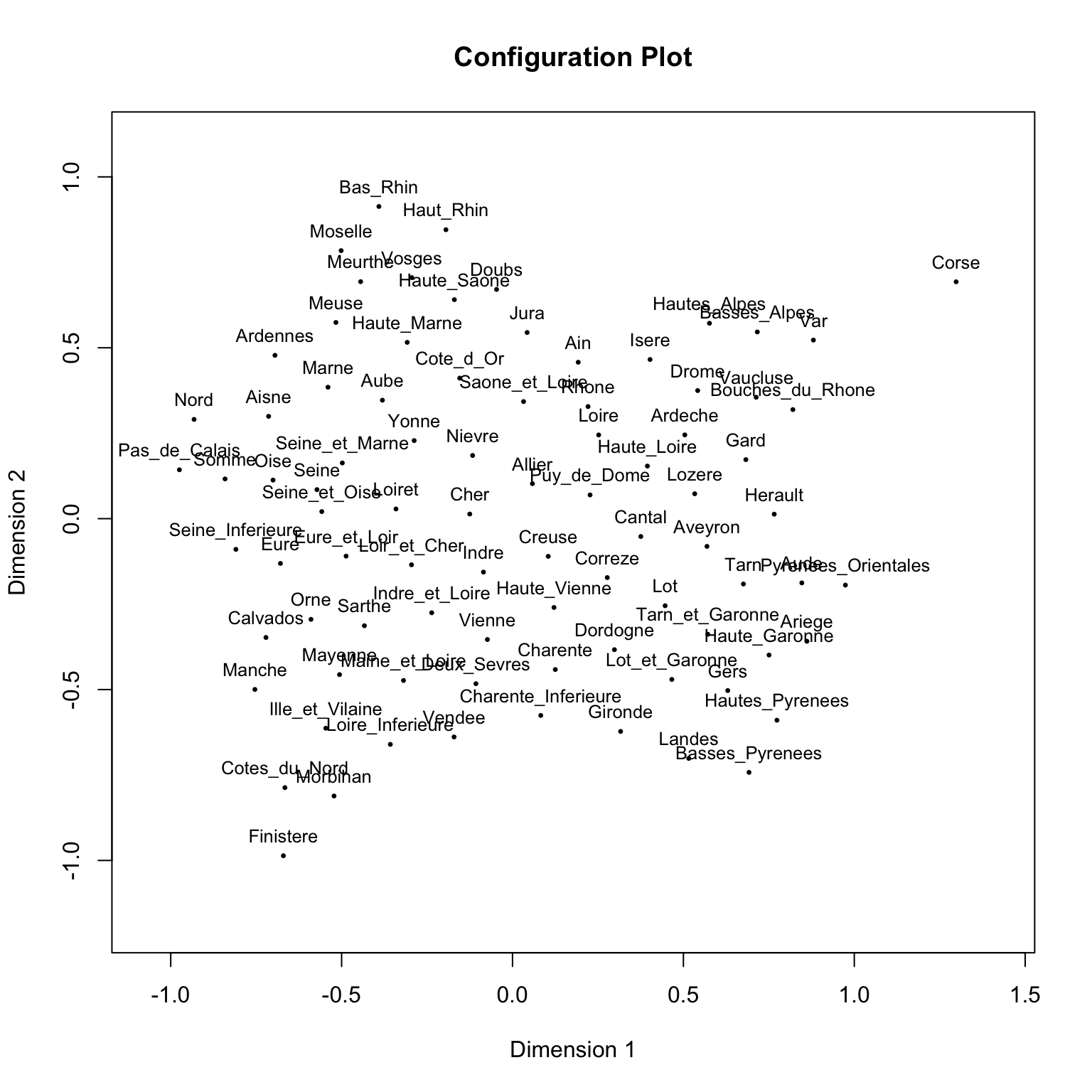
我们可以看到出现的图像近似于法国地图。

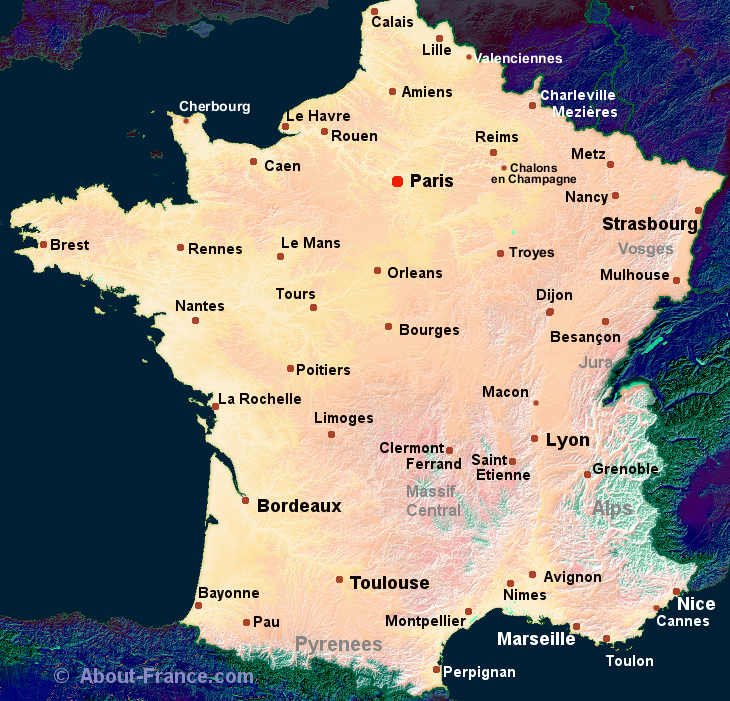
注意这里 MDS 图中的方向是任意的：这是这个方法的一个主要的限制。然而，不同的点的构型能够通过 Procrutes 算法的旋转从而得到相同的方向。

MDS 在神经表征相似性上的应用

现在我们来看一下如何在神经数据当中使用 MDS 方法。

# 对相似性矩阵进行命名
rownames(sqnsim) <- pnames
colnames(sqnsim) <- pnames

# flip sign and make positive
psqnsim <- -sqnsim
psqnsim <- psqnsim - min(psqnsim)

# fit MDS
mdfit1 <- smacofSym(psqnsim,2)
plot(mdfit1)

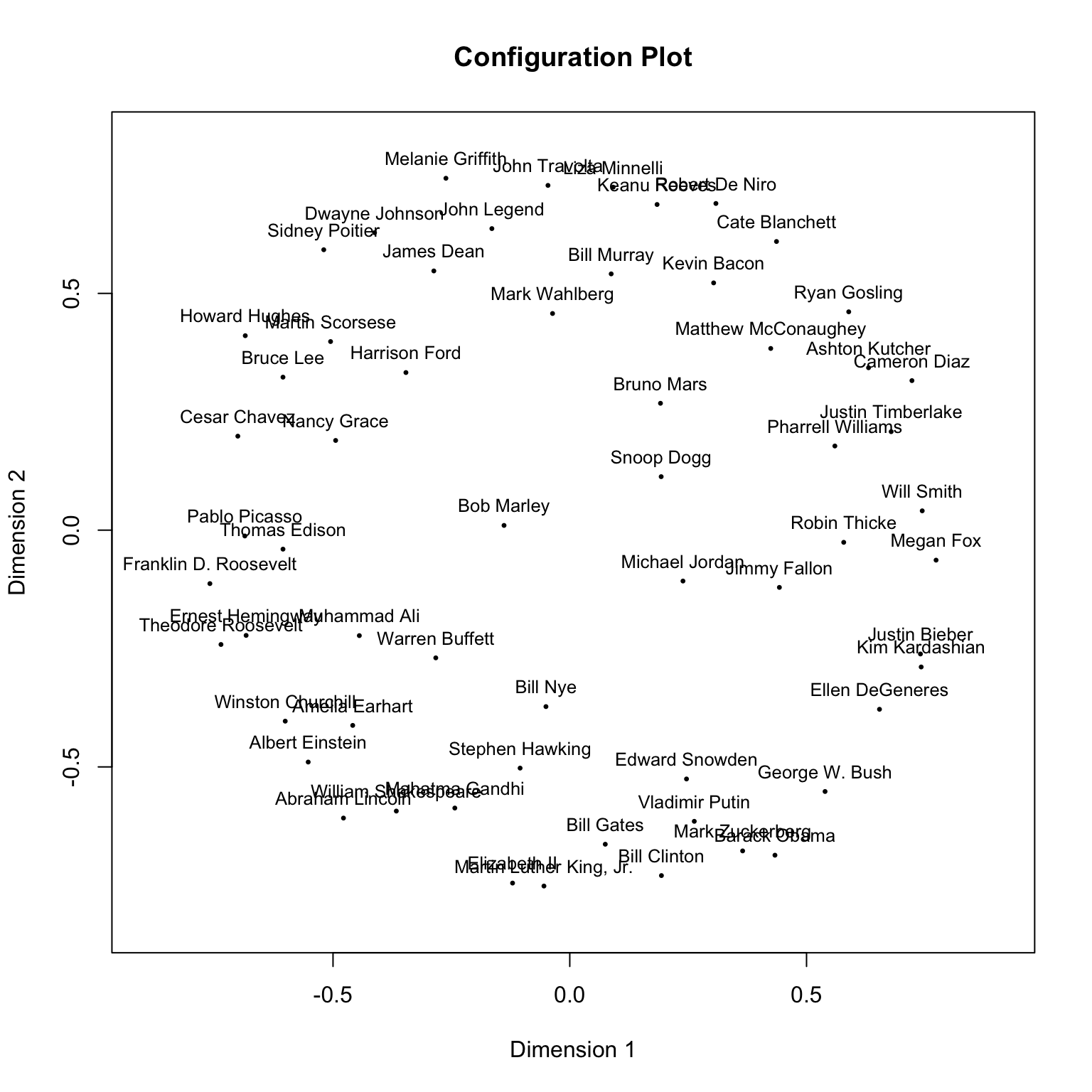
上图当中人物的距离越近，则意味着他们诱发被试的神经活动模式越相似。我们在什么情况下可以说这个构型对数据有着较好的拟合度呢？在 MDS 当中一个关键的估计统计值是“压力值”。它反映了构型当中的每一个点离它“应该在”的位置有多远。一个简单的标准是当压力值大于 0.15 时，结果较差。但是这并不是一个较好的方法，因为压力值极大地受距离矩阵中对象个数的影响。每节点压力值是一个更好的指标，因为它能够反映特定的点是否有较差的拟合。

mdfit1$stress

## [1] 0.3196393

plot(mdfit1,plot.type="stressplot")

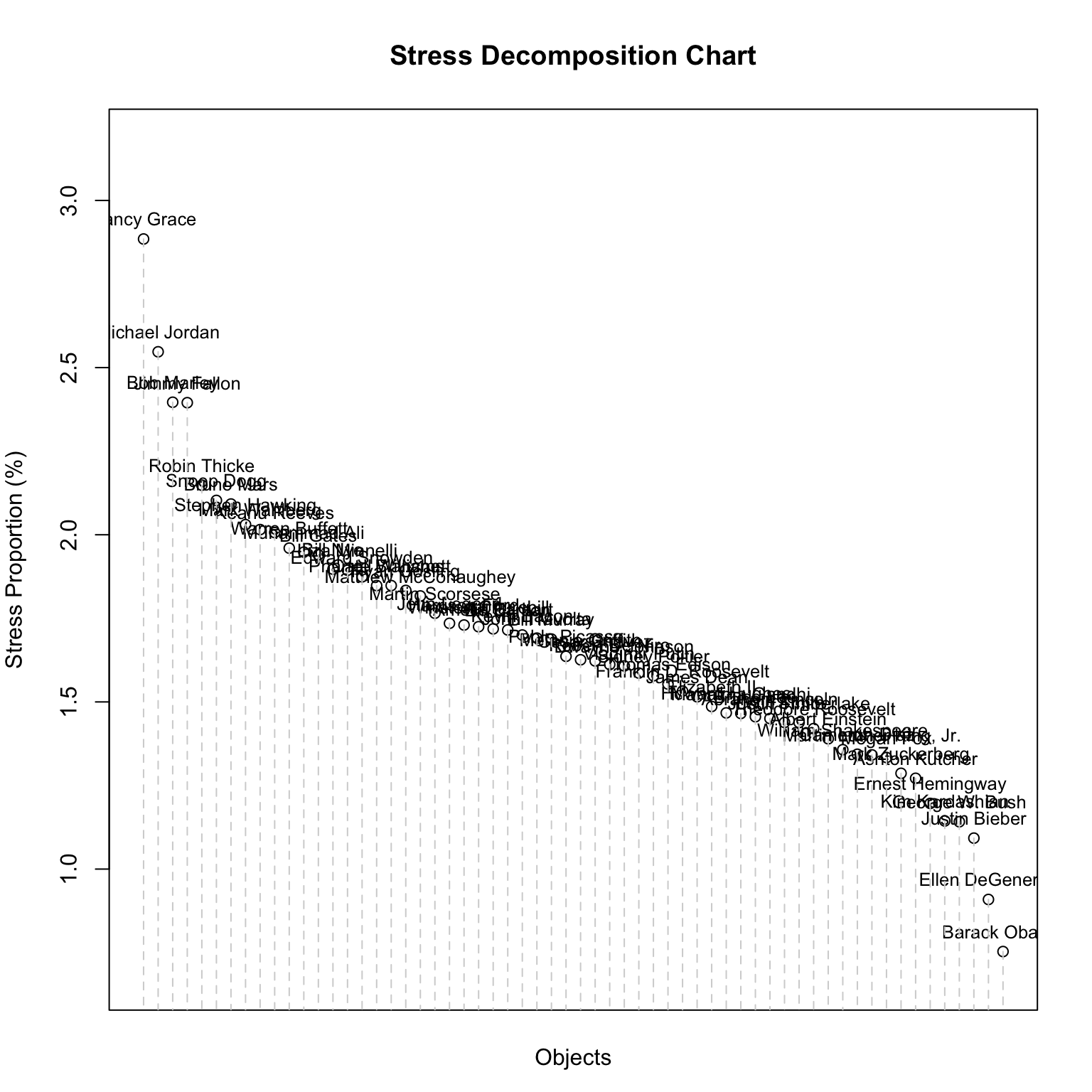
从上面的结果中，我们可以看到构型的整体压力并不是很好。 Nancy Grace，Michael Jordan，Jimmy Fallon 以及 Bob Marley 与其他个体的神经相似性相比，都在构型图中“放错了位置”。让我们尝试得到更好的拟合结果。我们在这里选择的方法是放宽我们的实验假设，将衡量相似性的度量变量看作是定序变量。

# fit MDS
mdfit2 <- smacofSym(psqnsim,2,"ordinal")
mdfit2$stress

## [1] 0.3086561

# Shepard plots are another helpful visual diagnostic to examine fit
layout(mat = t(matrix(c(1,2))))
plot(mdfit1,plot.type = "Shepard","Ratio fit")
plot(mdfit2,plot.type = "Shepard","Ordinal fit")

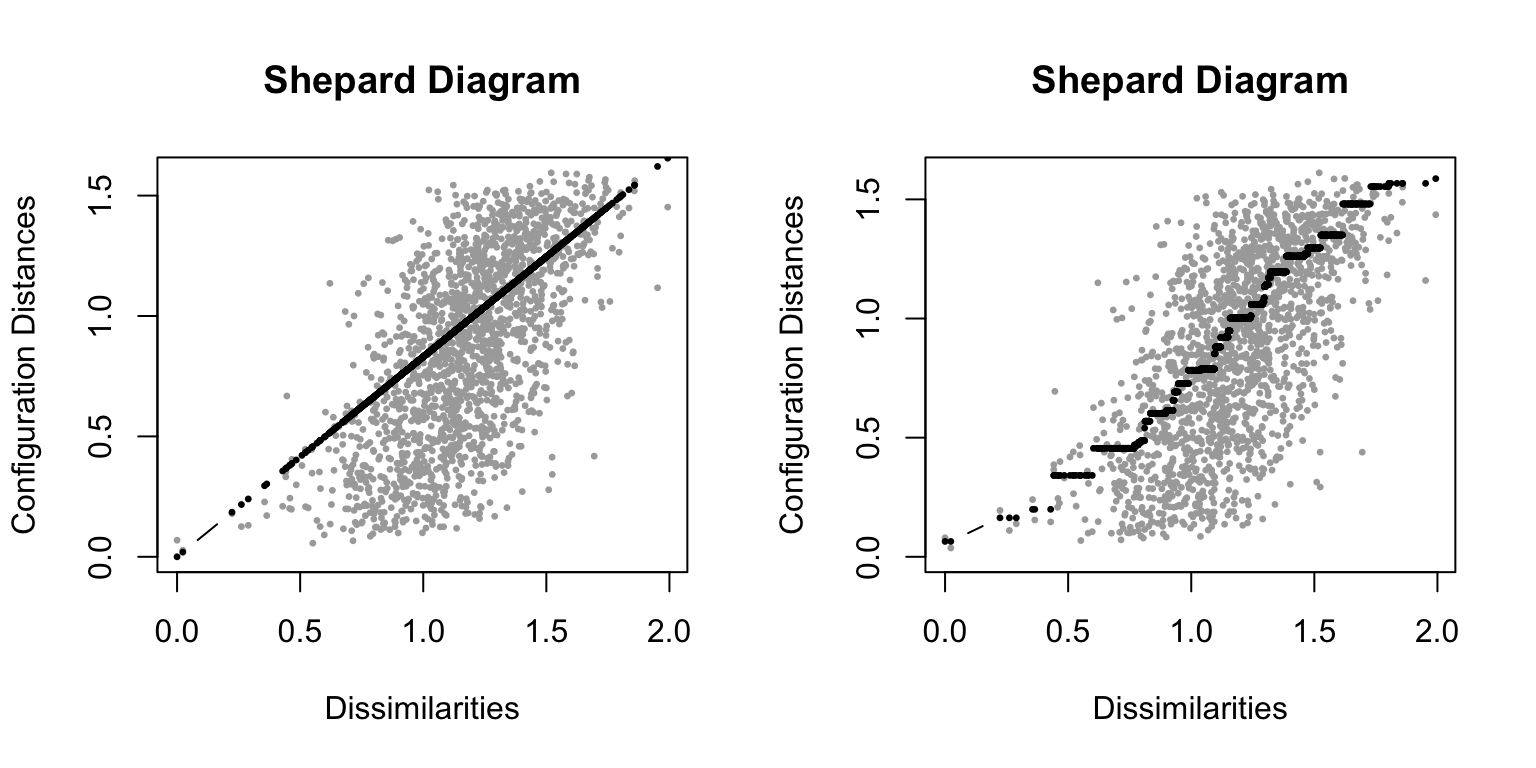
不幸的是，转换为定序的 MDS 并没有多大的帮助——我们的数据维度太高了，很难在2维上得到表征。稍后我们会介绍一下其他的流型学习方法来让结果变得更好。然而在这之前我们首先来看一下双标图：biplots. 正如我之前所提到的，MDS 的轴是任意方向的。双标图在 MDS 图上增加了一些箭头，这些箭头标示了每个维度在图中坐标轴方向上的相关性。这些箭头能够帮助我们理解 MDS 图背后的含义。

4.2 t-SNE

t-SNE 方法，或者说 t 分布随机近邻嵌入，是一种非常流行的流型学习和降维方法。不同于 MDS 尝试维持数据的全局结构，t-SNE 则是去保持数据的局部结构。因此在 MDS 当中，cluster 之间的长距离是存在意义的，但是很难保证最终得到的反映构型的近邻结果。相比之下，t-SNE 方法则在解释长距离时缺乏意义，但是近邻结构则会反映反映更多的数据含义。

# fit t-SNE and plot
set.seed(1)
tres <- Rtsne(as.dist(psqnsim),perplexity=4)
plot(tres$Y,pch=20,xlab="",ylab="")
text(tres$Y[,1],tres$Y[,2]+2,pnames,cex=.75)

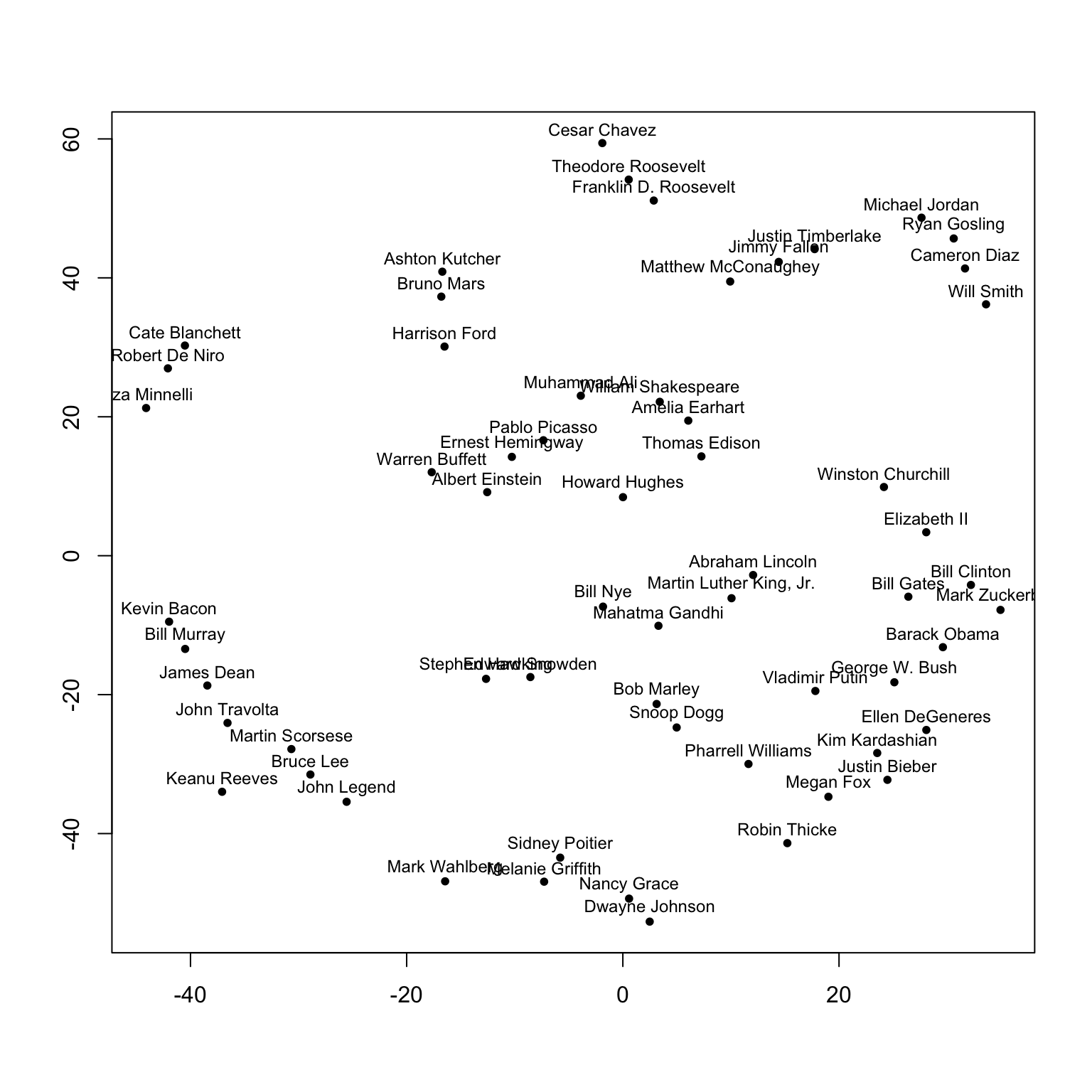
你能看到这里 t-SNE 的结果有点像聚类分析中的分类。事实上，在 t-SNE 当中存在“困惑度（perplexity）”这一参数，这个参数会影响最终做出聚类结果。在 这里这里提供一个教程，更为清晰地解释了 t-SNE 的参数设置和解释。

4.3 Hierarchical clustering

聚类分析是另一种探索相似性数据的技术，聚类本身是一个较为复杂的话题，因此我们在这里不会涉及太多的细节。但是让我们在这里简单看一下这种方法：多层聚类分析。它有着两种形式，包括将点聚集形成越来越大点簇（自下而上）和将簇分割成越来越小的点（自上而下）。两种形式都是直接对距离进行分析，而非对原始数据进行分析。同时，两种方法都会形成一个树状图（dendrograms）。点凝聚法相对来说更快，并且更常见，所以我们更多的是关注于这种方法。多层聚类分析由于其强大的呈现方式——树状图而对探索性数据分析有着巨大价值。

hc <- hclust(as.dist(psqnsim),method = "ward.D2")
plot(as.dendrogram(hc),horiz=T,xlim=c(4,-1))

结论

现在我们已经学习了如何对 fMRI 数据进行表征相似性分析。首先，我们学习了几种计算数据之间相似度的方法。接下来，我们了解了一些 RSA 相关的知识，包括NHST的方法，效应量，交叉验证和模型选择。最后，我们了解了几种探索和可视化数据相似性的技术，包括多维缩放，t-SNE 和多层聚类。这些方法结合在一起可以为你提供一个绝佳的角度开始分析数据相似性！